Age, Growth and Mortality of Terapon puta (Cuvier, 1829) in the Lake Timsah, Egypt

Teraponidae is a perciform family including 16 genera and about 48 fish species Nelson et al. and Minos et al., [1,2] which are frequent in the marine coastal, brackish and freshwater of the Indian and West Pacific oceans, including the Red Sea. 

Terapon puta is a medium size fish which inhabits the sea in Egyptian coasts. This fish has been popular as excellent sea food with a sensible market price. Though they are not commercially important, they constitute a regular fishery throughout the year. No information available regarding the growth studies of Terapon puta with the view of supplementing this, the present study was undertaken in the Lake Timsah, Egypt. 

In this study, it is expected to determine the age, growth rate, length- weight relationship and age composition of Terapon puta with von Bertalanffy growth models. Additionally, the natural and fishing mortality and the level of exploitation of this fish species off Lake Timsah were also estimated. The main aim of the present study was to shed light on some biological and dynamic features of the Terapon puta. Using such information is essential for the management and the good precision of the fishing in the lake Timsah.

A total of 335 specimens of Terapon puta were collected by monthly sampling between June 2012 and May 2013 from the landing site at Lake Timsah. Fishes were put immediately in crushed ice and transported to the laboratory, where they were subjected investigation. 

Age was determined by counting the annual rings on the scales using micrometer eye piece. In order study the time of ring formation to establish its annular nature, the scales representing rings under formation (growth checks) at the outer margin in different months were examined. To clarify further, the time of annulus formation, the distance from the last annulus to the margin of the scales were measured. A plot of monthly frequency of such scales which have marginal rings indicated the seasonal and established the annual nature. 

Length-weight relationship was obtained since the total weight of each fish specimen was given with a digital balance to an accuracy of 0.01 g and total length was measured with a precision of 0.01 cm. This relationship was determined according to the allometric equation given by Sparre et al., [3] as: 

W = a L^b

Where (W) is the total body weight in g, (L) is total length in cm; a and b are regression constants (Figures 1 and 2).

 

Figure 1: Showing Terapon puta (12.5 cm).

 

Figure 2: An scale from Terapon puta showing the ageing (Annual rings marked). 

 

Growth in length was expressed in terms of the von Bertalanffy equation:
Lt = L_∞ (1 - e^{- k(t - to)} )

Whereas (L) is the asymptotic total length, (Lt) is the total length at age (t), (k) is the growth curvature parameter and (to) is the theoretical age when fish is at zero total length. These growth parameters were estimated by means of von Bertalanffy plot Sparre and Venema [4]. 

Total mortality rate (Z) was estimated based on the length at first capture methods evaluated by Beverton and Holt [5]. 

L_∞ - L_m
Z = K * (--------------)
Lm - LC
Where: Lm = The average total length of the entire catch.
LC = The length at which 50% of the fish entering the gear are retained Sparre et al., [3].

Instantaneous natural mortality rates (M) were estimated using the equation derived by Ursin [6] based on the mean total length where: 

M = W–(1/b)

W = Mean total length.
b = Constant of length weight relationship.
Fishing mortality rates (F) were calculated as the difference between Z and M (Z = F + M). The value of the average annual exploitation rate (E) was obtained by E = F/Z. 

A total of 335 specimens of Terapon puta were collected, ranging in size from 7.3-14.6 cm TL. The length frequency distribution is shown in figure 3. As can be shown in the figure 3 the 11 cm length group was the most common one. Length frequency distribution, minimum, maximum, mean length and weight values of Terapon puta for each age group were shown in table 1, the age of Terapon puta ranged from 0 age group to II age group and the most dominant age group was I of 37.01%. Total weight of the sampled individuals ranged from 9.24-54.52 g overall mean total length and weight were calculated as 10.73±1.04 cm and 28.90±1.72 g, respectively.

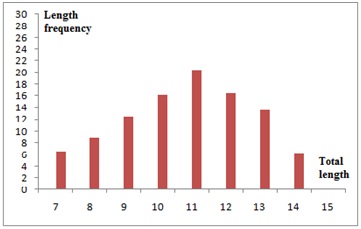Figure 3: Length frequency distribution for Terapon puta off Lake Timsah in Egypt.

Means the time at which a complete annulus is formed at the margin of the scale, this time is determined by using the marginal increment analysis or marginal growth which means the ratio between the distance from the last annulus to the margin and the total radius of the scale.

The mean marginal growth was calculated from scales for each month in order to establish the time of annulus formation which is shown in table 2 and represented graphically in figure 4 for Terapon puta. From table and figure it is indicated that the annulus formation occur in the month of Apr. and this means that the annual rings were formed in the period of spring.

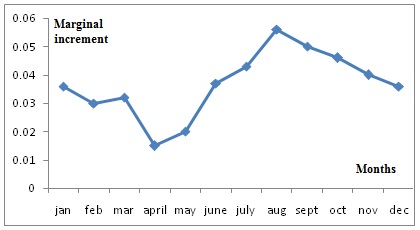Figure 4: Monthly record of marginal growth for the scales of Terapon puta of Lake Timsah in Egypt.

Month	Jan	Feb	Mar	Apr	May	June	July	Aug	Sept	Oct	Nov	Dec
No. of Fishes	10	12	9	10	9	10	7	9	11	13	10	10
MarginalIncrement(mm)	0.036	0.030	0.032	0.015	0.020	0.037	0.043	0.056	0.050	0.046	0.040	0.036

Table 2: Monthly variations of marginal increment of the scales of Terapon puta from the Lake Timsah, Egypt.

The age distribution of samples ranged from 0 age group to II age group for Terapon puta, based on the results of scales reading. The age group I was dominant (37.01%) followed by age groups 0 (35.22%), II (27.76%).

The growth of the studied fish was described by the von Bertalanffy model Von Bertalanffy [7] based on the back-calculated length at age data (Figure 5). The estimated growth function was:

 

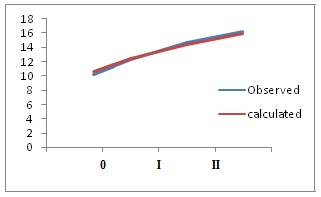Figure 5: The von Bertalanffy growth curve of Terapon. puta in the lake Timsah, Egypt.

L_t = 17.18 cm (1 - e^{-0.3632 (t +1.9363)})

The growth constant (K) was estimated at 0.3632. However, the maximum theoretical length (L_∞) and t0 describes the theoretical age where L_t is zero were 17.18 cm and -1.9363, respectively.

The result of a plot of scale radius against total length is revealed that a linear relationship exists between the radius of the scale and the body length and can be expressed as follows:

L = 3.19644 +1.48960 S (r = 0.996)

Where L is the total length in cm and S is the scale radius in mm.

The following formula was derived to obtain the back calculated total length at the end of each year of life for Terapon puta

LN = (L – 3.19644) Sn / S+3.19644

Where: LN is the length at the end of n^th year, SN is the radius of the scale to n^th annulus, S is the total radius of the scale and L is the total length at capture. From the data given in table 3, it is obvious that, Terapon puta attains its highest growth rate in the first year of life, after which a gradual decrease in growth increments was noticed with further increase in age.

Age Group	MeanNumber	ObservedLength (cm)	Back Calculated Lengths
			1	2	3
0+	119	7.5	8.2
I+	124	11.8	8.4	11.46
II+	93	14.3	7.4	11.18	13.8
Average total	335		8.0	11.63	13.8
Increment of length			8.0	3.63	2.17

The total length of Terapon puta varied from 7.3 to14.6 cm while the total weights ranged between 9.24 to 54.52 g. The equations were extracted for describing the relationship between weight and length as follows: W = 0.023425 * L^2.88 (r² = 0.98) or Log W = - 1.6303204+2.88 Log L Where: W is the total weight (gm), L is the total length (cm) and r is the correlation coefficient. The high values of r² indicate a good measure for the strength of these equations and closeness of observed and calculated values of fish weight. The length and weight measurements of the analyzed specimens used to describe the length-weight relationship are given in figure 6.

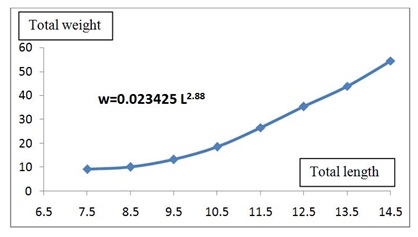Figure 6: Length- weight relationship of Terapon puta off Lake Timsah in Egypt.

The calculated weights at the end of each year of life of Terapon puta were estimated by applying the corresponding length-weight equation to the back calculated lengths. The resulting values are given in table 4.

Age Group	MeanNumber	Mean ObservationWeight (gm)	Back Calculated Weights
			1	2	3
0	119	10.13	8.71
I	124	31.69	11.27	28.47
II	93	45.15	10.70	29.63	42.69
Average total	335		10.22	29.05	42.69
Increment of length			10.22	14.17	17.96

Table 4: Average back-calculated weights (gm) of Terapon puta from the Lake Timsah, Egypt.

The obtained results indicated that the growth rate in weight was slow during the first year of life. Then the annual growth increment in weight increased with further increase in age until it reached its maximum value at the end of the third year of life.

By using the cumulative curve of Terapon puta (Figure 7) illustrating length at first capture at 50% and applying the method of Sparre et al., [3] the total mortality coefficient (Z) was estimated. This coefficient was found to be 1.49882 year^-1. But the Natural mortality coefficient "M" which obtained from the mean total length was 0.43220 year ^-1. Using the estimated (M) and (Z) the Fishing mortality (F) was obtained (1.06662 year^-1), where Z = M+F.

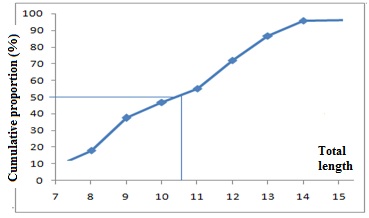Figure 7: Cumulative curve from which length at first capture was determined.

According to Gulland [8] which suggested that the optimum exploitation rate in an exploited stock should equal approximately 0.50. The current exploitation rate "E" was estimated at 0.71. Accordingly, the high value of the current exploitation rate indicates that the stock of Terapon puta in the Lake Timsah is subjected to overfishing.

The length at first capture L50% (the length at which 50% of the fish are first exposed to capture) was estimated as a component of the length converted catch curve analysis (FISAT), was found to be 10.6 cm which corresponds to an age of two years.

Age is one parameter necessary to assess population dynamics and the state of exploited resources Allain and Lorance [9]. The small scaled fish is not long lived; the maximum age of Terapon puta was 3 years. The same result was recorded by Sabrah et al., [10] when concluded that Terapon puta is a short life span fish (maximum 3 years).

Age and back-calculated growth were determined from annual rings in the scales. Increase in length is rapid during the first year and slow thereafter. This study showed that the mean annual growth rate for 0+-II+ year's old fish ranged between 2.17 and 3.3 6 cm (Table 3).

The result of the growth rate in the first year of the small scaled Terapon puta reported in the present study is 8.0 cm. The same result may be obtained by Sabrah et al., [10]. The largest individual caught in the Lake Timsah were 14.6 cm Similar observation was made by Sabrah et al., [10] concluded that based on the number of rings on the otoliths, the oldest fish were 2 years old (14.2 cm) recorded in Lake Timsah. While Allen and Swainston [11] in Australia reported 16.0 cm as a maximum total length of Terapon puta. 

The present study on the length-weight relationship of Terapon puta from the Lake Timsah coast has been studied. It is known that the relationship between length and weight has been studied in different fish species all over the world. The (b) values in fish is species specific and varies with sex, age, seasons, physiological conditions, growth increment and nutritional status of fish Bagenal and Tesch [12]. The relationship between total length and total body weight of Terapon puta was revealed highly correlation (r2 0.98) and the relationship was computed as w = 0.023425 L^2.88. It is clear that the growth in weight of Terapon puta in lake Timsah was characterized by negative allometric growth (b < 3).The same result was obtained by Karna and Panda [13] who concluded that the value of exponent (b) of Terapon puta in Chilika Lagoon, Odisha (India) equal 2.76 as well Sabrah et al., [9] prove that the value of (b) of Terapon puta in Lake Timsah, Egypt equal 2.72. Also Nandikeswari and Sambasivam [14] finished to the exponent (b) equal to 2.0246 for males and 2.2074 for females. It is clear that, if b < 3, then large specimens have changed the body shape to become more elongated or small specimens were in better nutritional condition at the time of sampling Froese [15].

The von Bertalanffy growth parameters were estimated using scales of Terapon puta in Lake Timsah, Egypt (L_∞: 17.18 cm, K: 0.3632 year^-1 and t₀: -1.9363 year). While the value of parameters reported by Sabrah et al., [10] was as L_∞: 15.5 cm, K: 0.7 year^-1 for Terapon puta in Lake Timsah, Egypt. The estimated parameters may vary as a function of a variety of factors such as region, year and methodology Goncalves et al. [16]. 

The exploitation rate of Terapon puta in the present study (E = 0.71) is higher than 0.50 of Gulland suggested that as a rule of thumb a fish stock is optimally exploited at a level of fishing mortality that generates E = 0.50 where optimum fishing mortality equal the natural mortality (F = M). Therefore, the stock of small scaled fish (Terapon puta) from the lake Timsah is being acutely over-exploited such observation noted also from the lake Timsah by Sabrah et al. [10]. The estimating total and fishing mortality rates in the lake Timsah with the exploitation rates were very high.