Determination of Shale Microstructure from Laboratory Data on Permeability

Shales are often related to unconventional reservoirs containing hydrocarbon, which makes them of interest for prospecting geophysics. Shales are also important as barriers to fluid flow in the reservoir overburden. Therefore, the problem of permeability estimation in shales is of vital importance. Many laboratory and field experiments show that shales are anisotropic rocks, and the anisotropy of their physical properties is caused by the preferential orientation of the structural elements composing shales (commonly, by preferential orientation of clay platelets and cracks) [1-7]. The crack alignment in the bedding plane correlated with the clay platelet alignment results in anisotropy of the hydraulic permeability of shales [8-10]. In this case the shales are of Vertical Transversely Isotropic (VTI) symmetry, and the shales permeability is described by the permeability tensor having two different diagonal components in the principal coordinate system. Additional systems of vertical and subvertical cracks existing at field scale lead to lower symmetry, and the permeability tensor in the principal coordinate system has three different components. In this case, shale is related to the orthorhombic symmetry.

At the scale of laboratory measurements (2 - 5 cm), the permeability of samples from Barnett Shale a gas shale formation (>60% carbonate,>20% Quartz and <20% Clay), located in the Bend Arch-Fort Worth Basin, Texas USA) measured in one direction on differently oriented samples give a possibility to reconstruct the permeability tensor. In this paper, we show such a reconstruction. However, these measurements require a complicated apparatus, special techniques depending on the rock type, and are rather time consuming. Another problem is to predict the permeability at another scale, for example, at the seismic scale. These facts lead to necessity of using theoretical methods to predict the permeability of anisotropic rocks. 

Different theoretical approaches exist for estimating the hydraulic permeability of rocks at different scales. At the pore (or core) scale (microscale), the most popular are the empirical approaches, which relate the permeability with porosity and grain or pore size [11]. At this scale, using the Poiseuille’s and Darcy’s laws, Gueguen and Palciauskas [12] derived simple formulas for calculating the permeability of isotropic porous medium containing uniform distribution of capillaries having not greatly varying radii and lengths. They also derived similar formulas for cracks of known and not greatly varying aperture and diameter. This approach linearly relates the permeability and porosity both for capillaries and cracks. Another approach presented by Gueguen and Palciauskas [12] is based on the notion of hydraulic radius that is the ratio of pore volume to pore surface. This approach allows one to derive formulas relating the permeability and porosity for different pore/crack shape (tubes or cracks) taking into account the pore/crack density in terms of the percolation factor. In the case of capillaries, the permeability is the function of the squared porosity. For cracks, the permeability depends on the cube of porosity. The well-known Carman-Kozeny equation also follows from this approach. The formulas of this approach are semi-empirical since they contain a parameter to be fitted from the experimental data. The approaches for permeability determination at the mesoscale (when the size of a heterogeneity is much greater than the pore scale) are the topological theory, percolation theory, renormalization approach, homogenization approach, and geostatistical approach [13-20]. The approaches based on Effective Medium Theory (EMT) were used both at the core scale and at the mesoscale [21-25]. To date, this question: “Is the EMT suitable for the permeability calculation at this scale or not?”, is really debatable (a discussion at 13IWSA meeting). As follows from the empirical formulas, the permeability is controlled by size of grains, and the EMT does not incorporate these parameters. Thus, from this point of view, the EMT seems to be inapplicable to the permeability determination at the core scale. According to Vogel [13], who considered the permeability determination at different scales using the topological methods, the permeability is controlled by different parameters at different scales. Thus, Vogel [13] showed that the principal parameters controlling the permeability at the pore-scale level are the pore/crack connectivity and distribution of the pore volume over pore diameter. At the larger scale level, where a medium containing a set of pore and crack could be considered as macroscopically homogeneous (i.e., effective), the permeability is mainly controlled by statistical parameters of the hydraulic conductivity (mean and variance) and two-point correlation function of the hydraulic conductivity. Vogel [13] wrote that at this scale level, the pore-size effects are smeared by the statistical characteristics of their conductivity. The EMT does operate with the statistical characteristic, and from this point of view, the EMT is applicable at scales greater than the pore-scale level. The EMT was applied to determination of permeability at the mesoscale by Neuweiler and Vogel [23,25]. They employed the classical self-consistent scheme. More advanced approach of EMT to calculate the hydraulic permeability at the mesoscale, the T-matrix method of the quantum scattering theory, was applied by Jakobsen [24]. The T-matrix method allows one to take into account interactions between all pairs of inclusions (two-point approximation). This makes it possible to incorporate in the solution different spatial statistics (in the form of ellipsoids) for different types of inclusions. Note that the paper of Jakobsen [24] also contains a lot of references to recent works on permeability estimation in heterogeneous media.

Commonly, when applying EMT to calculate the effective permeability of a porous cracked medium at the mesoscale, the real medium is replaced by a patched medium with patches having different values of permeability. Pozdniakov and Tsang [23] and Jakobsen [24] considered the permeability of a sand-shale mixture taking the hydraulic conductivity 1 m/d for sand patches and 1e-4 m/d for shale patches. Neuweiler and Vogel [25] treated a porous-cracked medium like a material consisting of even five patches with different hydraulic conductivities. In this approach the size of patch is much greater than the pore/crack size, and EMT is applicable as follows from the topological models.

When applying EMT at the core scale for calculating the effective elastic properties and thermal or electrical conductivity, the medium is assumed to consist of two components: mineral material and voids. If we formally apply EMT to calculate its effective permeability from the properties of these components, we meet more difficulties as compared to the case when the permeability is calculated at the mesoscale or to the case when other effective properties (mentioned above) are calculated. Thus, a question about the permeability of solid matrix and fluid arises. Since the permeability is a characteristic of the pore/space geometry, the permeability of fluid through itself should be extremely large, and the permeability of mineral matrix (without pores and cracks) should be zero. However the contact of mineral grains is imperfect and, thus, the mineral matrix should not have zero permeability. Besides, according to empirical theories, the rock’s permeability at the core scale depends on the pore size. This means that if we formally apply the effective medium theory to two rock samples of the same porosity, pore/crack shape, fluid filling the pore space, and mineral composition but having different pore/crack size, we obtain the same results, which is not correct. Xu and White [21] proposed an estimate for the void’s permeability when applying the effective medium theory at the core scale. They use the value equal to  as an intrinsic permeability of a flat fluid-filled spheroidal inclusion, where a is the inclusion’s size, and is the aspect ratio. This result is based on the fact that the intrinsic permeability of two parallel plates, a distance b apart, is .

 

In this work we apply the generalized singular approximation method of EMT to calculate the effective permeability of shale at the core scale. We consider shale as a two-phase medium consisting of mineral matrix and fluid inclusions. The matrix permeability has non-zero value, since the grain contacts are imperfect. We do not estimate the “fluid” permeability from the void’s size and shape, because we assume that the surface type (hydrophilic or hydrophobic) also affects this value [26]. We consider the “fluid” permeability as unknown parameter and invert it from experimental data. In the next section, we invert the permeability of matrix and “fluid” of three shale samples based on generalized singular approximation method of effective medium theory. In other words, we replace a rock at the core scale by a patch medium. One type of patches is associated with the mineral grains, and the other type is related to pores and cracks. The permeability of the two types of patches is assumed to be unknown. We invert the patch’s permeability values from the laboratory measurements together with the geometrical characteristics of the pore- and crack-related patches. The geostatistical approach also includes an inversion of some parameters form available experimental data [19]. However, instead of microstructure parameters mentioned above, these parameters characterize variances and correlation lengths of the permeability field.

Note that a good review of many methods and approaches for calculating the equivalent permeability of a heterogeneous porous medium can be also found in Renard P and de Marsily G [27] .

Review of the some recently published papers related to our goals can be found in Kefey Lu, et.al.,[28], Aslan Gassiyev et.al [29] and Xianfu Huang , Ya-Pu Zhao [30]. In the last paper authors measured connectivity parameters and distinguish between isolated and connected porosity which is extremely important for permeability estimations.

In general, the permeability is pressure dependent. The dependence of permeability on pressure occurs if the fluid flow is rather fast and the Reynolds number is non-negligible. It may occur when the fluid is gas. In this case the permeability obeys the Forcheimer law or Klinkenberg law [12]. However, if the fluid flow is rather slow, and the Reynolds number is much smaller than unity, the Darcy law applies, which linearly relates the fluid flux and the pressure gradient. Another reason of the pressure dependence of permeability is that the pore/crack geometry change due to the loading. Some samples show a dependence of permeability on the hydraulic gradient due to Bingham plastic flow within small pores [31]. However, we consider a “fixed” state of pore/crack geometry at a given effective pressure, and assume that this geometry does not change during the experiment on permeability determination.The porous cracked medium is a heterogeneous medium whose physical properties are coordinate-dependent. The local fluid flow in porous cracked medium obeys the Darcy law that has the form;(1)
where r is the vector in 3D space, q(r) is the coordinate-dependent vector of fluid flux (discharge per unit area, with units of length per time, m/s), k(r) is the coordinate-dependent permeability tensor (of the 2nd rank), µ is the dynamic viscosity of fluid, and is the local pressure gradient. If the flow is steady state and there is no sources and sinks,(2)
The Darcy law can be written in another form. If we introduce the hydraulic conductivity K by the formula (where ρ is the fluid density, and g is the gravity acceleration)(3)
We can rewrite (1) as follows;(4)

where  is called the hydraulic head (or, sometimes, tension). The hydraulic conductivity K is measured in m/s and depends on pore space geometry and fluid properties as well.We assume that the medium is statistically homogeneous, and we can specify so-called representative volume whose properties correspond to the effective properties of the medium under study. The tensor relating the fluid flux and gradient of hydraulic head averaged over a representative volume is called the effective tensor of hydraulic conductivity. The definition of the tensor of effective hydraulic conductivity has the form(5)
In formula (5) angular brackets mean averaging over the representative volume. A formal derivation of the effective hydraulic conductivity tensor using the generalized singular approximation method of the effective medium theory is given in Appendix. The formula for calculating the effective hydraulic conductivity has the form (see Appendix)

(6)

where tensor I is the fourth-rank unit tensor; tensor g depends on the inclusion’s shape and properties of the comparison body (see Appendix). Formula (6) includes the volume averaging. If the medium is statistically homogeneous, the volume averaging can be replaced by the statistical averaging (the ergodicity applies). We assume that all of the heterogeneities have the shape of general ellipsoid. The heterogeneities are assumed to be mineral grains and voids. If the heterogeneities differ in their physical properties, shape, and orientation in space, from formula (6) we have

(7)

 

where is the volume concentration of the i-th component; Ki is the tensor of hydraulic conductivity of the i-th component; is the distribution function of the inclusion’s volume over their shape characterizing by two aspect ratios χ_i1 and χ_i2 and Euler angles. We write formula (7) for two aspect ratios for one and the same permeability since below we use a double-porosity model to describe pore/crack geometry of shale. Note that formulas used by Pozdniakov and Tsang [23] incorporate so-called polarization tensor F instead of tensor g entering formula (7) for a general ellipsoid. The use of polarization tensor assumes that inclusions are ellipsoids of revolution. This, of course, simplifies the analytical formulas, but limits their applicability.In the derivation of formula (6) we assume that the comparison body is arbitrary. The choice Kc= K* gives the formula of self-consistent scheme [32,33]. If we consider a two-component medium whose components are pieces of mineral matter and another material (Material 1) having another (higher) permeability, the choices Kc= KM and Kc= KM1 where KM and KM1 are the hydraulic conductivity of the mineral matrix and Material 1 give, respectively, the lower and upper Hashin-Shtrikman (HS) bounds [34]. The lower HS bound corresponds to the medium when all inclusions of Material 1 are isolate, and the upper HS bound is related to the case when ellipsoidal pieces of mineral matter are inserted in Material 1. All intermediate cases are between the two limiting, as so, in our calculations we use the comparison body in the form of linear combination of KM and KM1:

 

(8)

We call the coefficient f in linear combination (8) friability. This empirical parameter can be treated as reflecting the degree of connectivity of Material 1. If the hydraulic conductivity of the matrix and Material 1 differ significantly, the HS bounds can be rather wide. Figure 1 shows the HS bounds calculated for a two-phase material with spherical inclusions. The hydraulic conductivity for the matrix and inclusions are taken as 1 and 10-4 m/day. This corresponds to the hydraulic conductivity of sand and shale [23]. Shale occupies 15% of the total volume. The effective hydraulic conductivity is also calculated for different values of friability entering expression (8). A strong non-linearity in dependence of effective hydraulic conductivity on friability is observed.In what follows we apply the generalized singular approximation method for calculating the permeability at the core scale. In so doing, we model a porous/crack rock by a patched medium consisting of patches related to mineral grains and Material 1. Material 1 replacing the pores and cracks has a finite (but rather high) scalar permeability.

 

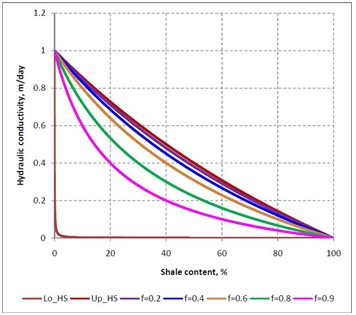Figure 1: Effective hydraulic conductivity of sand-shale mixture versus shale content. “Lo_HS” and “Up_HS” are, respectively, the lower and upper Hashin-Shtrikman bounds, f is the friability (see formula (8)).

The permeability was measured on three gas-shale samples. The apparatus called Permeability and Elastic Wave Velocities Shale Testing Apparatus KVST was used for these measurements. Plugs cut in different directions relative to the shale’s symmetry axis have the diameter and length of 2.54 by 2.54cm, respectively. The preparation of these plugs was described by Mohamed [8]. This apparatus allows one to simultaneously measure the permeability and elastic wave velocities (Vp and Vs) at variable applied and pore pressure. In the experiment the permeability and velocities are measured simultaneously using three cells. Every cell contains a sample cut in specific direction. The goal of this apparatus is the inversion of stiffness tensor and permeability tensor of shales that are, in the general case, of Vertical Transversely Isotropic (VTI) symmetry. For the stiffness tensor inversion, three samples are needed, whose axes are at 0, 45 and 90 degrees relative to the symmetry axis of shale. For the inversion of permeability tensor, two samples (cut at 0 and 90 degrees relative to the bedding) are sufficient. 

The confining and pore pressure were 41.4 and 20.7MPa, respectively. According to our thought most of the cracks in gas shale studied are similar to tension racks. Thus, Walsh [35] approach (P_e = P_c-0.56 P_p) is used to calculate the effective pressure. Meanwhile, this approach gives the best fitting with the cubic κ-α law (where α is the stress) for the pressure range used in the current study. This effective pressure corresponds to the initial effective pressure in field, during water injection (hydro fracturing) of the gas shale formation from which these samples were taken. The liquid permeability values obtained for Sample 1 are 5, 12 and 21nano Darcy in the direction normal to bedding, 45° to bedding, and parallel to bedding, respectively. The respective values for Sample 2 are 22, 38 and 71nano Darcy for these directions, respectively. While these values for Sample 3 were 4, 8 and 15 nano Darcy. The average mineral composition of the samples studied are (in mass %): quartz 40%, carbonate (calcite and dolomite) 25%, total clay (illite, mixed layer and kaolinite) 27%, other minerals (pyrite, apatite and plagioclase) 8%. The measured porosity of the samples 1-3 are 5.9, 6.7 and 7.3%; the density is, respectively, 2.68, 2.61 and 2.64 g/cm³. The difference in permeability measured in different directions is attributed to the effect of horizontal cracks which are favorable for the fluid flow in the bedding plane and slower the fluid flow normal to bedding (Figure 2).

 

Figure 2: Scanning electronic microscope photographs show thermo-mature gas shale microstructure. 

(A) Normal to the bedding views show platy minerals alignment parallel to the bedding; looking down on the basal planes of the clay particles. Unconnected discrete pores are seen (white arrow). 
(B) Parallel to the bedding view shows the well developed preferred orientation of the particles (alignment of platy minerals) and pores(white arrow).

The permeability measurements allow us to reconstruct the permeability tensors for these samples. Since the bedding plane is the symmetry plane, the permeability in this plane is independent of the azimuth and the components of the permeability tensor κ₁₁ κ₁₁ and κ₂₂ are equal to one another. The permeability measured normal to bedding gives the value κ₃₃ of the tensor. If the diagonal components of the permeability tensor are known, the permeability for any direction specified by the direction cosines n₁, n₂, n₃ is calculated by the formula [36]:



Since for each of three samples we measured permeability at the angles 0, 45, and 90 degrees relative to the vertical axis of the samples (which is associated with the symmetry axis), we can check if the permeability is really related to the VTI symmetry. In order to do this, we find the values k₁₁ and k₃₃which simultaneously produce the best fit to permeability measured in the three directions (0, 45, and 90 degrees relative to the vertical axis). To find the values, we apply the least mean square method. The shale’s permeability changes only in the normal-to-bedding planes. The dependences of permeability on the polar angle are same for all normal-to-bedding planes. Figure 3 presents the permeability calculated by formula (10) with the values k₁₁ and k₃₃ producing the best fit to the experimental data. The maximum difference is seen for 45 degrees and varies from 6 to 15%. The difference in the experimental and theoretical permeability for 0 and 90 degrees is less than 5%. We should take into account these errors if we use VTI symmetry to characterize the permeability of the samples.

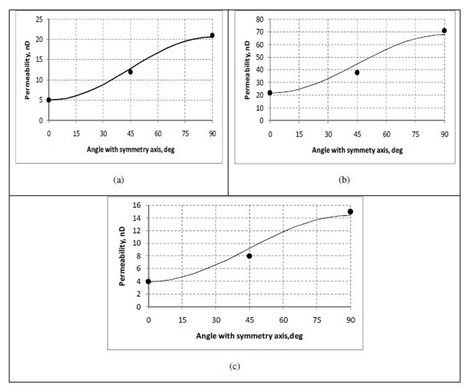Figure 3: The permeability distribution in the vertical plane calculated by formula (10) with the values κ₁₁ and κ₃₃ producing the best fit to the experimental data (solid curves). The experimental values are shown by circles. (a) Samples 1, (b) samples 2, and (c) samples 3.

To apply formula (7) to calculate the effective permeability of shale samples, first, a shale model should be constructed. We consider that shale is a substance containing mineral material and fluid inclusions in a form of ellipsoids of revolution. We assume that the fluid inclusions are of the two types: grain-related pores and aligned thin cracks. The latter are well seen under the electronic microscope. Thus, the total porosity is the sum of “pore porosity” (the relative volume of sample occupied by pores) and “crack porosity” (the relative volume of sample occupied by cracks). 

We assume that unknown parameters of shale’s microstructure entering formula (7) are as follows: friability, permeability of patches of solid material and “fluid” inclusions, crack porosity, aspect ratios of ellipsoids characterizing the patches of solid material, pore-related patches, and patches related to thin horizontal cracks. These parameters are found by minimization of the functional;

The summation in formula (11) is performed over the number of measurements. The parameters producing the minimum value to functional (11) are taken as characterizing the microstructure of shale’s samples. Formula (3) is used to recalculate the hydraulic conductivity into the permeability. Since the number of the inverted parameters is much greater than the number of measurements (only three directions), the permeability values obtained by formula (10) are also taken for the inversion as experimental ones. For each sample, we calculate the permeability values with a step of 5 degrees and as a result we have 19 “measurements” of permeability in the polar plane. Since the solution of any inverse problem is nonunique, in the minimization, we use physically reliable bounds for the sought-for parameters. We assume that the hydraulic conductivity of the solid material and “fluid” is, respectively, in the range 10^-12 - 10^-11 m/s and 10^-9 - 10¹⁰ m/s. The aspect ratio of the horizontal cracks varies from 0.001 to 0.05. The aspect ratios of solid grains and silt-grain-related pores change, respectively, in the ranges 0.001 - 1 and 0.05 - 1. The friability varies from 0.7 to 0.99. Note that this range of friability is commonly used to calculate the effective elastic properties of shale [37]. The crack porosity is assumed to be between 0 and 1%. This range for crack porosity follows from petrophysical analysis of sedimentary rocks [38]. We also include the total porosity in the list of inverted parameters allowing it to vary within ±2% from the experimental value. To minimize functional (11), we use the direct search complex method of optimization included in the Microsoft Fortran numerical library (IMSL) that is included in Compaq Fortran, version 6.6. During the optimization, we collect all solutions giving the difference between the experimental and theoretical values of permeability no more than 5% for the bedding plane and normal to the plane and no more than 15% for other directions. Then, the parameters in the selected solutions are averaged, and the average values are taken as the final solution. Table 1 lists the average values of the parameters (i.e., final solutions) with standard deviations for all of the three samples.

Sample	“Matrix” permeability, nD	“Fluid” penne ability, nD	Friability	Crack- patch aspect ratio	Crack porosity, %	Grain- patch aspect ratio	Pore- patch aspect ratio	Pore porosity, %
Sample 1	9.4e-19±1.1e-19	498±34	0.78±0.009	0.02±0.001	0.31±0.02	0.17 ±0.04	0.85 ±0.02	4.7±0.07
Sample 2	1.3e-18±1.4e-19	1359±76	0.82±0.01	0.02 ±0.002	0.51±0.04	0.24 ±0.04	0.66 ±0.03	5.5±0.12
Sample 3	6.2e-19±1.0e-19	225±14	0.81 ±0.01	0.009±0.001	0.37 ±0.05	0.20 ±0.05	0.69 ±0.04	7.2 ±0.09

 Table 1: The parameters of microstructure of shale samples inverted from the permeability measurements.

As seen, the “matrix” permeability is of the order 10^-19-10^-18 nano Darcy, and the “fluid” permeability range is 10^-3-10^-4 nano Darcy. The friability changes from 0.78 to 0.82. The aspect ratio of patches related to cracks is 0.01 - 0.02, and that for pores is 0.7 - 0.9. Grain patch aspect ratio varies from 0.17 to 0.2. This rather low aspect ratio of mineral-grain patches is explained by the fact that in our model we use a unified characteristic for silt-size grains that are isometric and clay platelets that are very thin. The crack porosity varies from 0.3 to 0.5%.

Note that the effective stiffness tensor and such tensor of thermal, electrical conductivity, and permittivity can be calculated from a formula similar to (6) [22]. However, for the elastic properties the tensor g is of the fourth rank and has the form,

 

where  is the stiffness tensor of comparison body;  ,  and  are the semi-axes of the ellipsoidal inclusion, and  .In order to validate the solution, we use the found parameters of shale microstructure to calculate the elastic wave velocities for these samples and compare them to the velocities observed in acoustic logs available for this formation. For this well, logging data on porosity, density, and mineral composition are also available. Since the samples were taken from another well, we find the depth for which the porosity, density and mineral composition are close to those of the samples under study. The density and porosity for the selected depth are 2.62 g/cm³ and 5.3%, respectively. The mineral composition is: quartz 43%, calcite 22%, and clay 35%.The effective stiffness tensor of shale is calculated in two steps. At the first step, the stiffness tensor of mineral material is calculated. To do this we insert isometric pieces of silt-size mineral aggregates into the clay matrix and apply a formula similar to (6) but with the comparison body having the properties of clay assuming that the pieces of silt-mineral polycrystals are isolated. The velocities and density of polycrystals of silt-size minerals composing the shale samples and taken for the calculations are shown in table 2. They were calculated from the tensors of respective monocrystals using the self-consistent method of effective medium theory, i.e., for the stiffness tensor of comparison body equal to effective stiffness tensor [32]. The clay is mostly illite for this formation, and we take the components of stiffness tensor of illite found by Bayuk et al., [39] for in situ conditions (in GPa): C₁₁= 127.4, C₃₃= 54.7, C₄₄= 14.4, C₆₆= 39.7 and C₁₃= 28.4, and density is equal to 2.7 g/cm³. At the second step, we construct a model similar to that used for the effective permeability calculation. We make a composite consisting of ellipsoidal inclusions of pores, cracks, and mineral material whose properties are found at the first step. At the second step, the stiffness tensor of comparison body is calculated by formula similar to (8) (with friability found from the inversion).The water saturation for this depth interval is 0.4 and we take this value for our calculations. The compressional wave velocity and density used for brine are 1.6 km/s and 1.1 g/cm³, and those for gas (methane) are 0.5 km/s and 0.001 g/cm³. When calculating the effective stiffness tensor at in situconditions (effective pressure is 30 MPa, and temperature is around 70 C°), we neglect a change in properties of constituents, since the change is not too significant. The elastic wave velocities Vp and Vs are calculated in the vertical direction (Vp_z and Vs_z) are compared with sonic velocities (Table 3). Note that in VTI medium, two shear waves (Vsv and Vsh) propagate with the same velocity along the symmetry axis, and we denote this velocity Vs_z. The maximum difference (6% for Vp_z and 12% for Vs_z) is observed for Sample 1 whose density differs much greater from logging density compared to other samples (the density for Sample 1 is 2.68 g/cm³). For the other two samples the difference in velocities attains a few percent. Note that the difference in velocities also results from the fact that the physical properties are different at different scales. For the elastic wave velocities this difference may be as high as 20 - 25% [40].We also calculate the velocities in the lateral directions (Vp_x and Vsh_x, Table 3) and compare them with those measured in the bedding plane in laboratory for samples taken from similar formation. Figure 4 shows the experimental data reported by Dyaur et al.[41]. As seen, the theoretical values obtained for the lateral direction are in good correspondence with those marked by ellipses in the plot shown in figure 4.

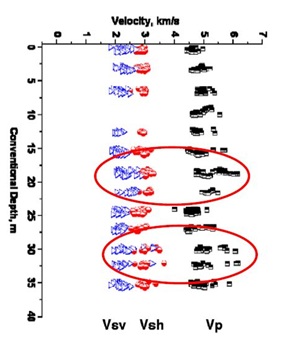Figure 4: Measurements of Vp and Vs velocities along the well in the bedding plane of the Barnett Shale collection. These results show that all the samples are anisotropic. The average shear wave splitting is 30% [41].

Mineral	Reference for corresponding stiffness tensor	Vp, km/s	Vs, km/s	Density, g/cm3
Quartz	McSkimin et al. [42]	6.02	4.06	2.65
Calcite	Peselnik and Robie [43]	6.54	3.35	2.71
Dolomite	Ahrens [44]	6.4	3.46	2.86
Albite	Belikov et al. [45]	6.01	3.29	2.62
Pyrite	Ahrens [44]	7.86	5	5.02

Mineral	Reference for corresponding stiffness tensor	Vp, km/s	Vs, km/s	Density, g/cm3
Quartz	McSkimin et al. [42]	6.02	4.06	2.65
Calcite	Peselnik and Robie [43]	6.54	3.35	2.71
Dolomite	Ahrens [44]	6.4	3.46	2.86
Albite	Belikov et al. [45]	6.01	3.29	2.62
Pyrite	Ahrens [44]	7.86	5	5.02

The found parameters of shale microstructure are also used for a prediction of thermal conductivity for in situ conditions. Note that the thermal conductivity is a parameter which is not measured in wells like elastic wave velocities or resistivity. Therefore, such a prediction is of practical interest. Table 4 lists the thermal conductivity of minerals used for the prediction. The thermal conductivity of minerals and fluids is more sensitive to temperature compared to elastic properties. The thermal conductivity of fluids is also affected by pressure. This fact forces us to use the thermal conductivity of constituents at the respective PT conditions (effective pressure is 30 MPa and temperature is around 70 C°). The thermal conductivity for pyrite is taken for the normal conditions, since data at elevated PT conditions are unavailable for this mineral. We take into account the anisotropy of thermal conductivity of illite which is structurally similar to muscovite. We use Horai [46] data for the thermal conductivity of muscovite along the optical axis a and assume that the value along the axis b is the same. The thermal conductivity of illite along the optical axis c is calculated from the ratio of thermal conductivities of muscovite along the axis a and c given by Clark [47]. We also assume that the thermal conductivity of illite changes insignificantly with temperature like for clays presented in Material Properties Database [48]). When calculating the effective thermal conductivity we use the two-step model described above. The thermal conductivity of water and methane are taken equal to 0.68 and 0.0714 W/(m•K), respectively [49]. The theoretical prediction of effective thermal conductivity distribution in the vertical plane is shown in figure 5. The resulting in situ thermal conductivity is highly anisotropic. The thermal conductivity of shale samples in the bedding plane is 4.0 - 4.6 W/(m•K), whereas the value normal to bedding is around 1.8 W/(m•K). The ratio of thermal conductivity in the bedding plane to that normal to bedding is as high as 2.5. If we neglect anisotropy of illite and take the average value for thermal conductivity of isotropic illite equal 1.68 W/(m•K), the ratio decreases almost twice, down to 1.3. In this case, the thermal conductivity in the bedding and normal to bedding is around 4.2 and 3.3 W/(m•K).

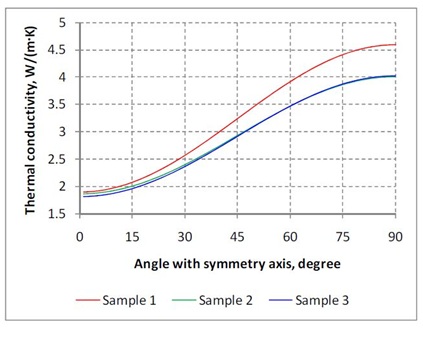Figure 5: Theoretical prediction of the thermal conductivity distribution in the vertical plane.

 

Mineral	Reference for corresponding stiffness tensor	Vp, km/s	Vs, km/s	Density, g/cm3
Quartz	McSkimin et al. [42]	6.02	4.06	2.65
Calcite	Peselnik and Robie [43]	6.54	3.35	2.71
Dolomite	Ahrens [44]	6.4	3.46	2.86
Albite	Belikov et al. [45]	6.01	3.29	2.62
Pyrite	Ahrens [44]	7.86	5	5.02

The inverted values of “fluid” and “matrix” permeability and other microstructure parameters can be used in further prediction of permeability for shale samples of similar mineral composition using the effective medium theory. For example, these values can be used for numerical analysis of different situations when an estimation of permeability change is required. Thus, Figure 6 exemplifies such an analysis. Figure 6a shows a change in components of permeability tensor for microstructure derived for Sample 1 but with varying porosity of pores from 0 to 15%. The porosity of cracks and shape of all constituents (pieces of mineral material, pores, and cracks) are assumed to be unchangeable and equal to those found with inversion (Table 1). Figure 6b shows the results of similar analysis but for varying porosity of cracks (from 0 to 1%); all other microstructure parameters do not change and are listed in table 1). Figures 6c and 6d demonstrate the ratio of permeability in the bedding plane to the value normal to bedding versus porosity of pores and cracks. This ratio is a measure of permeability anisotropy. As seen in figure 6c, the anisotropy decreases as porosity of pores increases irrespective of the fact that pores are not perfect spheres, and their aspect ratio is 0.85. The reason of such a behavior is that the relative amount of a component whose shape is the most isometric increases. One can also see that the anisotropy increases insignificantly if porosity of cracks having aspect ratio 0.02 changes from 0 to 1% (Figure 6d).

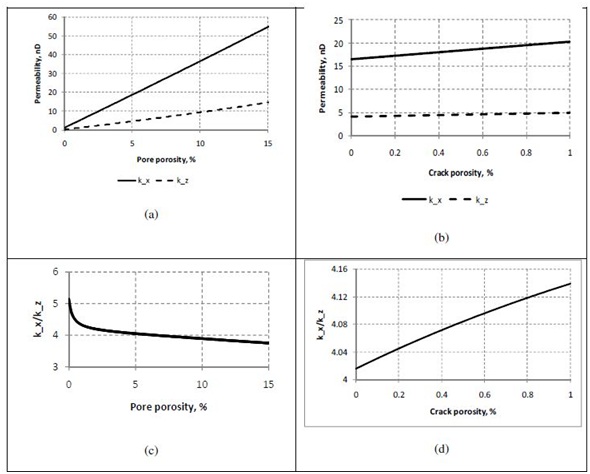Figure 6: Theoretical analysis of permeability variation with (a) porosity of pores and (b) porosity of cracks; (c) and (d) are variation of ratio of permeability in the bedding plane to that normal to bedding plane with porosity of pores and cracks, respectively.

To apply the effective medium theory for calculating the effective permeability of shale at the core scale, we replace the original rock by a patch medium that contains patches of two types: (1) mineral-matrix patches and (2) pore- and crack-related patches (“fluid” patches). The pore- and crack-related patches are assumed to have the same permeability but different shape (aspect ratio). The permeability of each patch type is inverted from the laboratory measurements of shale’s permeability together with other parameters incorporated in the shale’s double-porosity model: aspect ratio of patches related to mineral grains, pores and cracks and a parameter reflecting the pore/crack connectivity. The inverted “fluid” and “matrix” permeability can be further used in solving the forward problems on permeability determination of shales having similar mineralogy and compaction history. The inverted parameters of shale microstructure are used for prediction of anisotropic elastic properties and thermal conductivity at in situconditions. The elastic wave velocities predicted for the vertical direction are in good correspondence with those observed in sonic logs for close values of porosity, density and mineral composition. The velocities predicted for lateral direction are close to those measured in laboratory in the bedding plane of samples taken from this formation.