Spiral Induced Epileptic Seizures

In general, two types of neurons, excitatory and inhibitory ones, operate in the brain. The neurons of excitatory type, being connected to other neurons, transmit to them the command to operate, while the neurons of the inhibitory type transmit the opposite operation command. A neuron receiving information from both types, counts the numbers of each and decides whether to operate or not according to the dominance of either group. In a regular brain operation, the balance between these groups is about 4:1 in favor of the excitatory one. It is well known [1,2] that during epileptic seizures this balance is shifted towards a complete dominance of the excitatory group of neurons. In such situations modelling of the brain becomes mathematically similar to that of the heart in which no inhibitory cells exist, as both systems function by nonlinear transmission structures. We therefore assert that the elementary brain functions during epilepsy can be mathematically addressed under similar approaches as those used in heart analysis. Heart fibrillation is usually initiated by tachycardia, a fast operating heart. One of the prevailing views in the field is that the origin of these malfunctions is a spiral of Action Potential (AP) [3], rotating in some location of the heart and inducing adverse effects in the other parts of the organ. Consequently, to understand a possible origin for epileptic seizures, we would like to find out how the brain, when activated by an AP spiral, will function under excitatory neuronal dominance.

Many models of spiral waves in brain tissues have appeared in the literature. Using nonlinear dynamics theory to explain the transition from normal behavior to epileptic one is already found in daSilve et al. [4]. A similar approach to ours appears in Ursino and La Cara [5], who used a simple integrate and fire model to simulate brain activity. See this reference also for a thorough review of previous attempts to explain epileptic brain activity. In rare cases, Ursino and La Cara [5] found the appearance of spiral waves under very strict conditions.

Most of the existing mathematical models of the brain function are rather complicated [6]. The models are classified by the authors of Wendling et al. [6], into the following categories: Neural mass models, neural field models, detailed networks and formal mathematical models. Most of the models use both high complexity and a relatively massive size of the interacting entities in the system, in an attempt to approach the natural situation. We have opted to use a relatively simple reaction-diffusion model based on a 2D Morris-Lecar system. This model was chosen in accordance with the Occam-Einstein Razor guide, namely to use the simplest approach which can explain the phenomena but not too simple, so that the important facts are not lost. We will show that our choice is indeed an effective one.

The original Morris-Lecar (ML) equations, [7,8], were set up to model the behavior of a single neuron in an excitable medium. Many other authors [9,10] extended the model to include coupled neuron potential activities on a spatial lattice, usually 2D, as follows


Where V, W, and J are respectively, the membrane potential (the AP, called local field potential, LFP in the brain related literature), the recovery variable and the background stimulation current of each neuron. We use here the following values of the constant parameters (identical to those in) [9], excepting C:

 

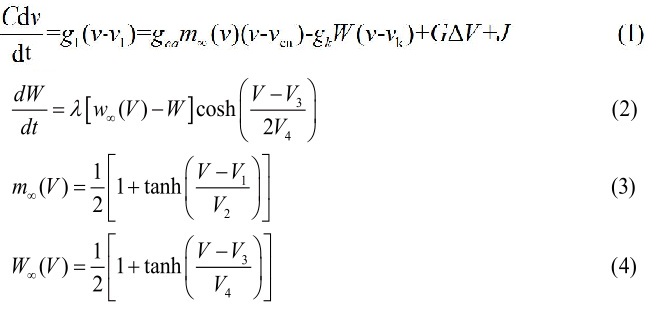
The dynamics is initiated at time t=0 by constructing a centrally located spiral profile (Figure 1) of the LFP, V (x, y, t), whose evolution in time is represented in figure 2. The spiral is initiated here by the “free edge” effect Biton et al. [11]. Adjacent lines of Action Potential (AP) and Refractory Period (RP) are set up as initial conditions. The AP line is slightly tilted beyond the RP one. As a result, the free edge of the AP line tilts even more and develops into a spiral.


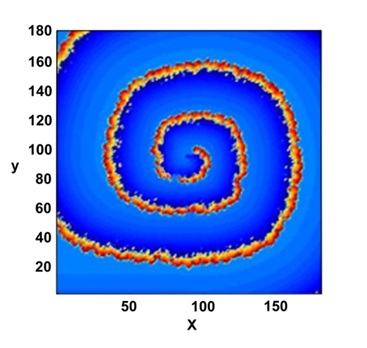
Figure 1: The lattice at time t=0. A rotating spiral is generated centered at x=y=0 2.

 

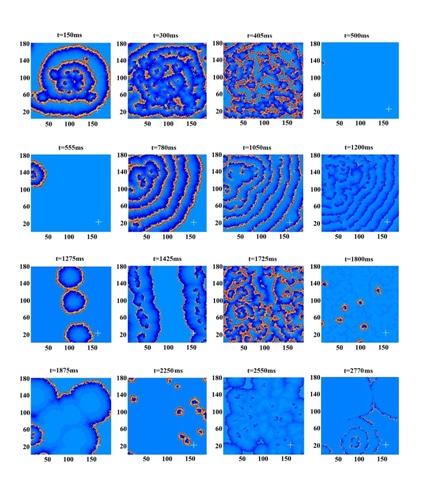
Figure 2: A set of selected, 2D maps of the potential V (x, y, t) observed a long time evolution. Probe center position marked by a cross.

After the spiral creation, the membrane stimulation current J=J₀ is kept uniformly constant at all times.

The conductance G, defined above, is the only physical parameter to be modified several times on the run. The following random changes of conductance (G) are meant to simulate time changes of the brain activity. This is done here, every time, by two simultaneously operated, random procedures, as follows: one procedure uses 8 preset, equally spaced, time interval values in the range (100, 380) ms., while the other is based on a set of 10 conductance values G between 0.05 and 0.85mS/cm². During the time evolution, each future time interval value is drawn randomly, at the end of the current one, from the uniform distribution of the elements in the interval set. Then, all 1802=32400 conductance values G are randomly reset in the following manner: Firstly draw uniformly one element from the set of G’s, which becomes the maximal G during this period of time. Next, construct a 180×180 matrix, containing randomly distributed positive numbers in (0,1). Finally, multiply this matrix by the drawn G, to obtain its distribution.

Figure 1 represents the spiral (rotor) generated on the lattice center at t=0. Results show that the spiral is only sustained only for a limited time. It deteriorates subsequently into multiple disconnected structures, which disappear and then reappear at various time and position points, forming and developing multiple target waves, double spirals (figures of eight), etc. These patterns may represent the turmoil in epileptic brain activity, illustrated here in figure 3 by the time series of the LFP at a specific single point (model electrode), arbitrarily located and indicated by the + position in figure 2. This particularly exhibited LFP time series, as well as any other one, chosen at will, appear to be rather spiky. To compare them to real EEG measurements in epileptic patients, a spatial average of LFP’s over 5×5 sites around the model electrode center at point + were calculated and shown in figure 3. This average is assumed to simulate the reading of areal electrode of equivalent size. Figure 4 is a real EEG measurement [10,12], by an electrode mounted on an epileptic patient. Structural similarities between the results in this work and those of Cao et al. [10], are apparent. 


Figure 3: Time series of V (t) at the probe center x=150, y=24 single point (upper frame, black), and the averaged values in its 5×5 neighborhood (lower frame, red).

 

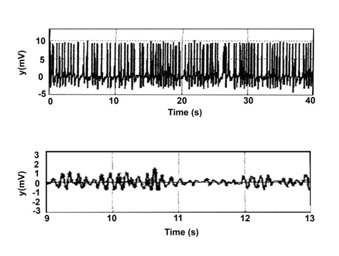
Figure 4: Time series of epileptic activities (modified from figure 3 c,d of Cao et al.) [10]. 

Note: similarity to forms of figure 3.

Regarding the possibility of a spiral being the epileptic driving force, we refer to the recent measurements reported by Viventi et al. [13], by using cortical surface electrodes recording from the exposed frontal lobes of cats in which electro graphic seizures were produced after GABA-mediated inhibition was inactivated by picrotoxin administration. These authors have shown that, at least for a limited period of time, spiral waves were observed on the brain surface during an epileptic ictal. Figure 5 compares the observed spiral to the core of the spiral of our model. Note that according to the present model the lifetime of the spiral is short which may explain its elusive behavior.


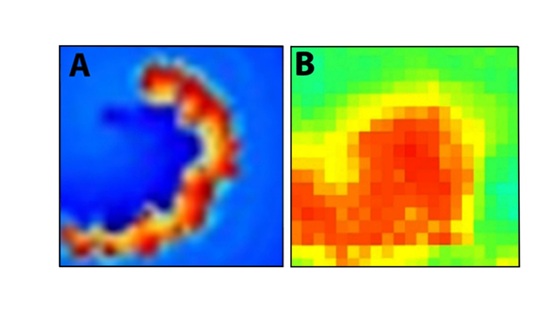
Figure 5: The core part of the model spiral. B: (adapted from figure 5b of Viventi et al. 2011) [13]. The snapshot of a spiral appearing during an epileptic seizure.

Also note that most of the recorded experimental results related to epilepsy rely on EEG measurements by a fixed number of electrical electrodes. Therefore, the spatial resolution of the outcomes is quite poor and observing a spiral or any other spatiotemporal phenomenon on the brain is almost impossible. Since using toxic voltage sensitive dyes on human brains is prohibited, it seems that direct measurement of spirals in human patients can be achieved only in the future. However, indirect effects as discussed here and animal models [13] do support our assumption.

The similarity of the obtained patterns here to those appearing in heart fibrillation is clear. Although our assumption was that these systems would behave in a similar manner, the actual results could not have been anticipated. Being based on such a crude model, these results should, of course, be taken with a grain of salt. Some inherent problems in using simple models to simulate the very intricate and complex brain behavior appear in Jun and Jun [14].

More experiments and calculations should be conducted in order to ascertain the validity of our assumption. For instance, it may be argued that spiral waves appear in the brain also during its regular function [15,16]; notably during a sleeping mode, not leading to a seizure; See also more recent spiral waves appearance in neural networks [17,18]. We think that a benign appearance of a spiral might be attributed to the existence of enough inhibitory neurons, which stop it in the bud in order to prevent malfunction.

In the heart, the havoc-causing spiral is thought to be initiated by a “reentry” or “re-entry circuit”, which deteriorates into a rotor. Some authors [19] postulate that a brain reentry circuit can by itself induce rapid oscillations in its vicinity, which are already the birthmarks of epileptic seizure. This assumption should be carefully investigated.

Finally, it is important to stress that the spiral action is the concluding driving force in the seizure genesis process. The necessary condition for the process is the reduction of the inhibitory neurons percentage [12].

1. A simple model (Morris Lecar) of a 2D brain tissue was studied under dominance of excitatory neurons. 
2. An initial spiral was introduced in the tissue and its neural connections were randomly changed according to several guidelines.
3. The ensuing 2D electronic patterns were calculated showing a breakup of the spiral and a recurrence of new shapes of local field potential on the tissue.
4. An “EEG” was detected at a specific location on the tissue both directly and as an average (“large” electrode) around the selected position.
5. The shapes of the “EEG’s” are shown to be similar to actual measurements in epileptic patients.
6. An actual spiral was experimentally observed during an epileptic seizure. 

It is thus suggested that, under excitatory dominance, a spiral could be an initiator of an epileptic seizure.

The authors would like to thank Professor R Thieberger and Mrs. S Rabinovitch for helpful discussions.

All authors report no conflict of interest.