
Effect of Cycling Field for Room Temperature Polarization of Multiferroic BiFeO3 Nanocrystals
*Corresponding Author(s):
Sangram Keshari PradhanCenter For Materials Research, Norfolk State University, 700 Park Ave., Norfolk, VA 23504, United States
Tel:+1 757 823 8765,
Email:skpradhan@nsu.edu
Abstract
Keywords
INTRODUCTION
The stoichiometric BFO exhibits a rhombohedrally distorted perovskite structure with space group R3c due to an antiphase rotation of the adjacent FeO6 octahedran [22] as well as G-type antiferromagnetic structure. In impurity free BFO, the off-center distortion originates from the stereo active lone pair of electrons of Bi3+ ions. The hybridization between Bi 6s and O 2p is responsible for generation of ferroelectric characteristic, and the super exchange interactions between Fe-O-Fe mainly dominate the magnetic ordered structure [23-26].
Although the macroscopic magnetization originated from the Dzyaloshinsky-Moriya (DM) interaction is permitting in R3c symmetry, a cycloidal spatially modulated spiral spin structure with a period of approximately 62 nm superimposed onto the G-type antiferromagnetic spin ordering, which cancels out any net magnetization [18,27-29]. Thus, the linear Magnetoelectric Effect (ME) is very weak, which limits its practical application. From an experimental point of view, room temperature ferroelectric behavior of BFO has proven to be a difficult task. In fact, electrical measurements are more sensitive to the presence of grain boundaries and impurities in BFO sample. Besides, secondary phases, high leakage current are also the crucial problems. These defects, presumably more conducting than the pure BFO sample, induce high leakage currents which creates more difficult for the application of high electric field on the sample and make the measurement of a hysteresis loop quite difficult. Recently, considerable researches have been focused on improving the ferroelctric and magnetic behavior through optimized synthesis technology, nanocrystallization, and the modification of chemical composition [30-32].
Pure BFO shows very less polarization value. However, theoretical studies using density functional theory predict that BFO can show a large ferroelectric polarization of 90-100 µCcm-2, [33] consistent with the atomic displacements of the Bi3+ and Fe3+ ions. This paper presents the polarization loops obtained at room temperature of pure BFO nanocrystal and their evolution under cycling electric fields as well as the different conduction mechanism and multiferroicity exhibited by the nanocrystals.
EXPERIMENTAL
Bismuth nitrate pentahydrate (Bi(NO3)3.5H2O) (99.99%) is dissolved in the 2- methoxyethanol and acetic acid mixture. After the solution is transparent, it is mixed with iron nitrate nanohydrate (Fe(NO3)3.9H2O) (99.99%) by constant stirring at room temperature. The resultant solution is transparent, blackish red and clear. The precursor solution is dried at 100?C for about 8 hour to obtain the BFO nanocrystals. Powders of above samples are palletized using poly vinyl alcohol as a binder. Cylindrical pellets having dimension 13 mm diameter and 2 mm thickness is prepared by hydraulic press. Final sintering of pellet is done at 800?C for 6 hours. For contamination free electrical contacts sample is polished with the same pellet to obtain thickness (0.1 mm).
X-ray diffraction pattern of the samples are carried out in the 2θ range (20?-80?) using Cu Ka radiation by Philips diffractometer (Model: 1715) fitted with monochromator operated at 45 kV and 40 mA. Microstructure image of the sample is obtained using Field Emission Scanning Electron Microscope (Hitachi-SU8000). Ferroelectric (P-E) measurement of sintered pellets is carried out using ferroelectric hysteresis loop tracer (Model: RT6000, Radiant Technology, USA). Dielectric measurement of pellets is done using LCR bridge (Quadtech, USA). Leakage current measurement is done using Keithley electrometer (Model 617). Capacitance-voltage characteristics are measured in the metal-ferroelectric-metal configuration using CV plotter (Model-4200-CVU). Magnetic measurement was carried out using SQUID Magnetometer (Quantum Design- MPMS).
RESULTS AND DISCUSSION
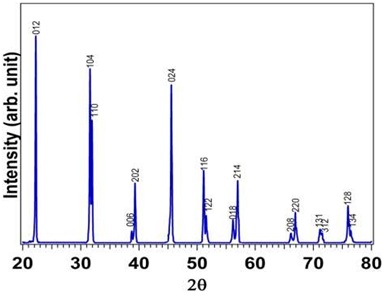
Figure 1: XRD patterns of BiFeO3 nanocrystal.
Microstructure analysis of BFO is carried out using FESEM as shown in figure 2. The FESEM image shows the formation of nanocrystal having densely packed crystallites of various sizes from few tens to few hundreds of nanometers which are almost homogeneously distributed and leaving relatively less scope for development of uneven and irregular pore structure inside the bulk region.

Figure 2: FESEM image of BiFeO3 nanocrystals.
In order to study the leakage phenomenon normally associated with BFO, J-E characteristics of the samples is carried at room temperature as shown in figure 1. J-E curves shows well defined symmetry around the current axis under the application of positive and negative voltage (±30kV). At lower electric field region, as shown in figure 3a, the leakage currents nature of the sample shows linear, indicating an Ohmic conduction behavior. But gradual increase in applied electric field the graph changes to a non-linear features, which suggests that there may be some other conduction mechanism associated with the conduction process such as Space Charge Limited (SCL), Schottky emission, Poole-Frenkel emission, etc. It is observed that the value of leakage current gets reduced significantly for the sample prepared through sol-gel route. An encouraging leakage current density value of 2.74×10−6A/mm2 was found in BFO nanocrystals which may be promising for multiferroic device application. As known, the cause of leakage current in BFO sample has been attributed to the small amount of Fe2+ ions and oxygen vacancies existing in the sample. oxygen vacancies normally appears from Bi volatility and the valence fluctuations of Fe ions from Fe3+ to Fe2+ which hinders the observation of good ferroelectric hysteresis loop in BFO bulk sample. But in case of nanoparticle BFO, suppression of above vacancies took place which also restricts the transformation of Fe from Fe3+ to Fe2+ with improved leaky behavior.
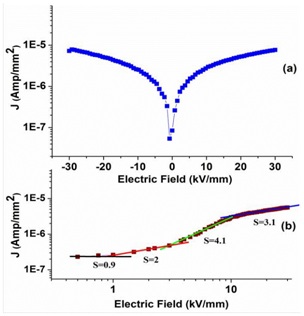
Figure 3: (a) Leakage current density as a function of electric field (b) Leakage current density fitted by space charge limited conduction theory of BiFeO3 nanoparticles sintered at 800?C for 6 hours.
According to the SCL theory developed by Rose [34] and Lampert [35] the log-log plot of current density versus electric field is fitted well by four linear segments with various slopes as shown in figure 3b. At low fields, the slope is close to 1 indicating a linear Ohmic conduction behavior, which is dominating by thermally stimulated free electrons. The leakage current for Ohmic conduction can be expressed as;
J=eµNeE (1)
Where µ is the free carrier mobility, Ne is the density of the thermally stimulated electrons, e is the electron charge, and E is the applied electric field. On further increase in electric field electrons will be penetrated in to insulator, and at sufficiently high applied field, the density of free electrons due to the carrier injection becomes more than the density of thermally stimulated electrons. Then the leakage current density follows the SCL law (modified Chield’s law) [35].
J=9εrε0µθV2/8d3 (2)
Where, V is the applied voltage, εr is the static dielectric constant, ε0 is the permittivity of free space, θ is the total density of d is the thickness of the sample and θ is the ratio of the total density of free electrons to the trapped electrons. The change of the slope to 2 is 4 kV/cm indicates the transition between Ohmic and SCL current behavior, and the transition voltage VSCL is given as;
VSCL = eNed2/2θεrε0, (3)
After the SCL current behavior, the abrupt increase in leakage current occurred because the applied voltage forces of all the available traps to become filled, which is the Trap Filled Limited (TFL) law. The abrupt increase in leakage current is shown by the slopes of 4.1 in figure 1b. The voltage at which this abrupt increase occurs is called trap-filled-limit voltage VTFL, and it is related to the density of traps by;
Where, Nt is the total trap density here, VTFL is 24 for the nanoparticles of BFO. Finally the slope becomes 3 which could be due to the combined effects of SCL and other field enhanced conduction mechanism [36]. Therefore, it is reasonable to conclude that the SCL conduction mechanism is dominant for the BFO nanoparticles synthesized by sol-gel route.
Frequency (100Hz to 2MHz) dependent room temperature dielectric properties (dielectric constant-“K” and dielectric loss-“tanδ”) of BFO nanocrystals are shown in figure 4. It is observed that both K and “tanδ” are strongly dependent on frequency and decreases in higher frequency region. But relatively at lower frequency region, dielectric constant strongly depends on frequency showing a dielectric dispersion evidently. Such as a strong dispersion seems to be a common feature in ferroelectric materials concerned with ionic conductivity, which is referred as low-frequency dielectric dispersion [37]. When the frequency increases, the relative effect of ionic conductivity becomes small and as a result, the frequency dependence of K becomes weak.
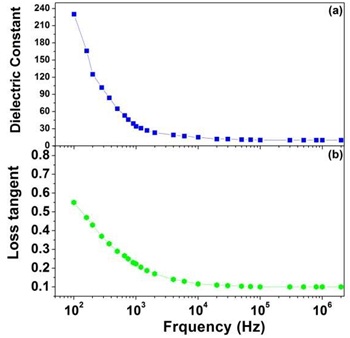
Figure 4: Room temperature dielectric constant and loss tangent as a function of frequency of BiFeO3nanoparticles sintered at 800?C for 6 hours.
As observed from figure 4a, dielectric constant of BFO nanoparticles at 100 Hz is 230. It is known that value of dielectric constant K at lower frequencies normally depends on the lattice vibrations, excitation of bound electrons, dipole orientation, and space charge polarization (atomic and electronics). At higher frequency region (104 Hz and beyond), the value of K is almost constant. This flat type characteristic at higher frequencies indicated that there is no space charge polarization contribution at the frequency range.
The dielectric loss curve behaves similar trend that of dielectric constant as shown in figure 4b. It shows the loss tangent value of less than 1 at lower frequency (100 Hz) region and gradually reduced to lower value then become constant at higher frequency region. It is reported [38] that, low dielectric loss at low frequency would reflect lower value of leakage current, which is technologically more important for the effective utilization of BFO nanoparticles in multiferroic devices application.
In order to study the ferroelectric property of the nanocrystal, polarization as a function of electric field measurement (Figure 5) is carried out at room temperature for several times in order to observe the reproducibility of the cycles as well as “fatigue” nature of BFO nanoparticles occurs if any. As ferroelectric materials are piezoelectric in nature, it is well known that mechanical stresses will induce by the application of cycling electric field leads to the degradation of the material property. The value of coercive field, saturation polarization as well as remnant polarization affected prominently due to the constraint of domain wall motion throughout the sample. As a consequence, the reliability of their electric switching is reduced and resulting to an increase of coercivity from 40 kV/cm to 49 kV/cm along with the slow degradation of saturation polarization value from 11 µC/cm2 to 10.6 µC/cm2. This phenomenon showed by the material is generally known as fatigue and gradually affect the electrical degradation of the compound under cycling electric fields above the coercivity.
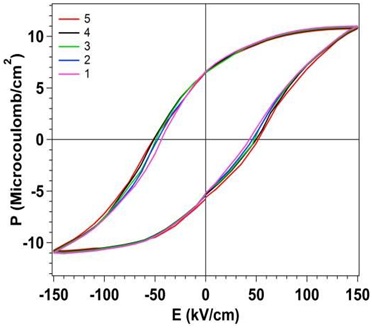
Figure 5: Gradual modification of the shape of (P~E) loops during electric field cycling of BiFeO3nanoparticles sintered at 800?C for 6 hours.
The capacitance-voltage characteristic is measured in the metal-ferroelectric-metal configuration using a small Alternating Current (AC) signal of 10mV at 100 kHz. The AC signal is applied across the sample, while the Direct Current (DC) was swept from positive to negative bias. C-V measurement of BFO nanoparticles was carried out with DC sweep voltage from +25 V to -25 V as shown in figure 6 and analyzed to corroborate J-E and P-E measurement. In C-V loop the voltage corresponding to capacitance peak is known as coercive voltage. The observation of butterfly shape C-V loop for BFO nanocrystal is obtained with decreasing and increasing voltage for both polarities. This behavior is related to the presence of ferroelectric domains, which is also clearly evident from polarization as a function of electric field hysteresis loop measurement (Figure 5).
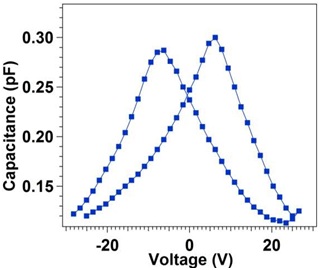
Figure 6: Capacitance as a function of applied voltage of BiFeO3 nanoparticles sintered at 800?C for 6 hours.
Room temperature magnetization as a function of magnetic field (M~H) of the sample is shown in figure 7. It is found that M-H graph of BFO nanocrystals shows the nonlinear trend resulting to formation of a narrow hysteresis loop. This observation clearly shows that BFO nanoparticles are the possible potential candidate to enhance the magnetic properties of BFO based multiferroic system. It is suggested that the size effect of BFO nanostructures might be responsible for the magnetic ordering. Basically BFO exhibits G-type antiferromagnetic structure by its origin with the wave length of the incommensurate cycloid spin structure of 62 nm [18] in bulk form cause zero net magnetic moment but the scale of nanosized BFO is comparable with this wavelength range. Now it is expected that, the enhanced magnetization value of perovskite structure of BFO may be the canted (non-collinear) arrangement of spins in the near-surface layers of the nanosized BFO. The effect of canted spins in the surface shell of BFO nanoparticles manifests itself by the uncompensated magnetic moments of Fe3+ ions, enhancing the tangible contribution to the particle’s overall magnetization. It is also expected that the spin cycloid structure along the magnetic axis is partially destroyed in the nanocrystal BFO, resulting observation of ferromagnetism at room temperature.
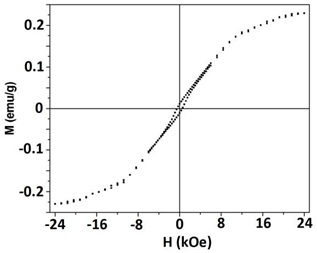
Figure 7: Room temperature Magnetization (M) as a function of magnetic field (H) of BiFeO3nanoparticles sintered at 800?C for 6 hours.
CONCLUSION
ACKNOWLEDGEMENT
REFERENCES
- Eerenstein W, Mathur ND, Scott JF (2006) Multiferroic and magnetoelectric materials. Nature 422: 759-765.
- Spaldin NA, Fiebig M (2005) Materials science. The renaissance of magnetoelectric multiferroics. Science 309: 391-392.
- Ramesh R (2009) Materials science: Emerging routes to multiferroics. Nature 461:1218-1219.
- Pradhan SK, Sahu DR, Rout PP, Das SK, Pradhan AK, et al., (2017) Chemical pressure induced change in multiferroicity of Bi1+2xGd 2x/2Fe1-2xO3 bulk ceramics. Physica B: Condensed Matter 510: 80-85.
- Zhao T, Scholl A, Zavaliche F, Lee K, Barry M, et al., (2006) Electrical control of antiferromagnetic domains in multiferroic BiFeO3 films at room temperature. Nature Materials 5: 823-829.
- Tabares-Munoz C, Rivera J-P, Bezinges A, Monnier A, Schmid H (1985) Measurement of the Quadratic Magnetoelectric Effect on Single Crystalline BiFeO3. Japanese Journal of Applied Physics 24: 1051-1053.
- Pradhan SK (2013) Raman and electrical studies of multiferroic BiFeO3. J Mater Sci: Mater Electron 24: 3581-3586.
- Arya G, Kotnala RK, Negi NS (2014) A Novel Approach to Improve Properties of BiFeO3Nanomultiferroics. J Am Ceram Soc 97: 1475-1480.
- Pradhan SK, Roul BK (2012) Electrical behavior of high resistivity Ce-doped BiFeO3 Physica B: Condensed Matter 407: 2527-2532.
- Chowdhury SS, Kamal AHM, Hossain R, Hasan M, Islam MF, et al., (2017) Dy doped BiFeO3 : A Bulk Ceramic with Improved Multiferroic Properties Compared to Nano Counterpart. Ceramics International 43: 9191-9199.
- Pradhan SK, Roul BK (2011) Effect of Gd doping on structural, electrical and magnetic properties of BiFeO3 J Phys Chem Solids 72: 1180-1187.
- Muneeswaran M, Giridharan NV (2014) Effect of Dy-substitution on the structural, vibrational, and multiferroic properties of BiFeO3 J Appl Phys 115: 214109.
- Pradhan SK, Roul BK (2011) Improvement of multiferroic and leakage property in monophasic BiFeO3. Physica B: Condensed Matter 406: 3313-3317.
- Moreau JM, Michel C, Gerson R, JamesWJ (1971) Ferroelectric BiFeO3X-ray and neutron diffraction study. J Phys Chem Solids 32: 1315-1320.
- Pradhan SK, Das J, Rout PP, Das SK, Mishra DK, et al. (2010) Defect driven multiferroicity in Gd doped BiFeO3at room temperature. J Magn Magn Mater 322: 3614-3622.
- Basith MA, Khan FA, Ahmmad B, Kubota S, Hirose F, et al. (2015) Tunable exchange bias effect in magnetic Bi9Gd0.1Fe0.9Ti0.1O3nanoparticles at temperatures up to 250 K. J Appl Phys 118: 023901.
- Park TJ, Papaefthymiou GCA, Viescas AJ, Moodenbaugh AR, Wong SS (2007) Size-dependent magnetic properties of single-crystalline multiferroic BiFeO3 Nano Lett 7: 766-772.
- Huang F, Wang Z, Lu X, Zhang J, Min K, et al. (2013) Peculiar magnetism of BiFeO3 nanoparticles with size approaching the period of the spiral spin structure. Sci Rep 3: 2907.
- Sosnowska I, Neumaier TP, Steicele E (1982) Magnetic properties of BiFeO3 micro-cubes synthesized by microwave agitation. J Phys C 15: 4835-4846.
- Dutta DP, Mandal BP, Naik R, Lawes G, Tyagi AK (2013) Magnetic, Ferroelectric, and Magnetocapacitive Properties of Sonochemically Synthesized Sc-Doped BiFeO3 J Phys Chem 117: 2382-1389.
- Pradhan SK, Das J, Rout PP, Mohanta VR, Das SK, et .al (2010) Effect of holmium substitution for the improvement of multiferroic properties of BiFeO3. J Phys Chem Solids 71: 1557-1564.
- Glazer M (1972) The classification of tilted octahedra in perovskites. Acta Cryst 28: 3384-3392.
- Hill NA (2000) Why Are There so Few Magnetic Ferroelectrics?. J Phys Chem 104: 6694-6709.
- Wang J, Neaton JB, Zheng H, Nagarajan V, Ogale SB, et .al(2003) Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures. Science 299: 1719-1722.
- Catalan G, Scott JF (2009) Physics and Applications of Bismuth Ferrite. Adv Mater 21: 2463-2485.
- Scott JF (2007) Data storage: Multiferroic memories. Nat Mater 6: 256-257.
- Dzyaloshinsky I (1958) A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J Phys Chem Solids 4: 241-255.
- Moriya T (1960) Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys Rev 120: 91.
- Sosnowska I, Neumaier TP, Steichele E (1982) Spiral magnetic ordering in bismuth ferrite. J Phys C Solid State Phys
- Ke X, Zhang P, Baek S, Zarestky J, Tian W, et al. (2010) Magnetic structure of epitaxial multiferroic BiFeO3 films with engineered ferroelectric domains. Physical Review B 82: 134448.
- Suresh P, Srinath S (2013) Effect of La substitution on structure and magnetic properties of sol-gel prepared BiFeO3. J Appl Phys 113: 17D920.
- Zhang X, Sui Y, Wang X, Tang J, Su W (2009) Influence of diamagnetic Pb doping on the crystal structure and multiferroic properties of the BiFeO3 J Appl Phys 105: 07D918.
- Neaton JB, Ederer C, Waghmare UV, Spaldin NA, Rabe KM (2005) First-principles study of spontaneous polarization in multiferroic BiFeO3. Phys Rev B 71: 014113.
- Rose A (1995) Space-Charge-Limited Currents in Solids. Phys Rev 97: 1538.
- Lampert MA (1956) Simplified Theory of Space-Charge-Limited Currents in an Insulator with Traps. Phys Rev 103: 1648.
- Chen F, Li B, Dufresne RA, Jammy R (2001) Abrupt current increase due to space-charge-limited conduction in thin nitride-oxide stacked dielectric system. J Appl Phys 90: 1898.
- Wang XX, Tang XG, Chan HLW (2004) Electromechanical and ferroelectric properties of (Bi1?2Na1?2)TiO3-(Bi1?2K1?2)TiO3-BaTiO3(Bi1?2Na1?2)TiO3-(Bi1?2K1?2)TiO3-BaTiO3 lead-free piezoelectric ceramics. Appl Phys Lett 85: 91.
- Yun KY, Noda M, Okuyama M, Saeki H, Tabata H, et al. (2004) Structural and multiferroic properties of BiFeO3 thin films at room temperature. J Appl Phys 96: 3399.
Citation: Pradhan SK, Sahu DR, Roul BK (2017) Effect of Cycling Field for Room Temperature Polarization of Multiferroic BiFeO3 Nanocrystals. J Laser Res Appl 1: 001.
Copyright: © 2017 Sangram Keshari Pradhan, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

