
Journal of Nanotechnology Nanomedicine & Nanobiotechnology Category: Medical
Type: Case Report
Perspective of Applying Adaptive Neuro Fuzzy Inference System (ANFIS) in Laser Cladding of Graphene-Metal Alloys
*Corresponding Author(s):
Hamed SohrabpoorDepartment Of Mechanical And Manufacturing Engineering, Dublin City University, Dublin, Ireland
Tel:+353 894224550,
Email:h.sohrab@outlook.com
Received Date: Jul 24, 2017
Accepted Date: Sep 13, 2017
Published Date: Sep 29, 2017
Abstract
Laser powder deposition is a potential nontraditional coating process which includes several of parameters that affect coating performance. Obtaining optimal parameters associated with better efficiency is substantial. Hence, it is proposed that using Adaptive Neuro-Fuzzy Inference System (ANFIS) can predict performance of graphene-metal alloys recently in order to reduce manufacturing process which increases the production efficiency and accuracy. In addition, according to many researches, graphene known as the worlds strongest known material that can improve nanotechnology products.
Keywords
ANFIS; Graphene; Laser powder depositions
INTRODUCTION
Laser cladding by lateral powder injections, is a surface coating that can enhance the metrological surface of the components. Recently, this process has been used for repairing and coating some critical components in industry. In this process, the powder/alloy is deposited laterally or coaxially on the molten pool which is produced by laser beam (with Gaussian energy intensity) [1]. The substrate surface is coated with overlapped clads to cover a large area. However, in Gaussian-beam laser cladding, the formed clad has a convex shape and can significantly reduce the aspect ratio. Dilution is another critical factor to be minimized during laser cladding process [2]. Figure 1a indicates schematic of feeding on laser cladding which location of powder nozzle is different and depends on characteristic of clad layer. For example, the major benefit of the discontinuous coaxial powder nozzle is the potential to tilt the deposition head without influencing the powder stream [3].
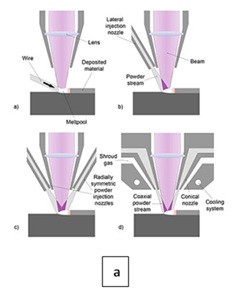
Figure 1: Schematic of feeding on laser cladding.
The ultimate goal to study the laser cladding of Graphene/metal alloys is to optimize the process in terms of single/multiple objectives [4,5]. Optimization can be defined as mathematically or statistically modeling the laser cladding process to optimize (to obtain the optimum) response based on the process parameters. Various modeling and optimization algorithms are used to optimize the said parameters. Artificial intelligence is a potentially strong technique to model the laser cladding process [6]. This modeling approach was applied to laser cladding of Graphene/metal alloys i.e., Graphene/graphene PVA film [4]. Optimization can be performed for single or multiple response parameters.
Previously, some researchers used ANN (Artificial Neural Networks) for prediction of their experimental works. For instance, Petkovi? et al., employed ANN in order to estimate the wind speed fluctuation based on the fractal interpolation [7]. In addition, they used ANFIS for designing and adaption of prediction of optimal power coefficient value of the wind turbines [8]. Moreover, they applied neuro-fuzzy approach to detect the most important variables which affect the wind speed according to the fractal dimensions [9]. Finally, they used ANFIS for prediction of how five parameters can effect on outputs the ANFIS network was performed to determine how the five parameters affect the wake wind speed [10]. In another article they adapted to estimate wind farm efficiency according to turbines number in wind farm [11]. Furthermore, Khademi et al., applied ANN, ANFIS and regression for prediction of strength of recycled aggregate concrete [12]. They are concluded that ANN and ANFIS are better in mix design optimization and in the case of higher accuracy requirements. After that, they used same models for prediction of 28 days compressive strength of concrete [13]. The results were similar in the case of using these models, when higher accuracy is needed, the ANN and ANFIS models are proposed.

Figure 1: Schematic of feeding on laser cladding.
The ultimate goal to study the laser cladding of Graphene/metal alloys is to optimize the process in terms of single/multiple objectives [4,5]. Optimization can be defined as mathematically or statistically modeling the laser cladding process to optimize (to obtain the optimum) response based on the process parameters. Various modeling and optimization algorithms are used to optimize the said parameters. Artificial intelligence is a potentially strong technique to model the laser cladding process [6]. This modeling approach was applied to laser cladding of Graphene/metal alloys i.e., Graphene/graphene PVA film [4]. Optimization can be performed for single or multiple response parameters.
Previously, some researchers used ANN (Artificial Neural Networks) for prediction of their experimental works. For instance, Petkovi? et al., employed ANN in order to estimate the wind speed fluctuation based on the fractal interpolation [7]. In addition, they used ANFIS for designing and adaption of prediction of optimal power coefficient value of the wind turbines [8]. Moreover, they applied neuro-fuzzy approach to detect the most important variables which affect the wind speed according to the fractal dimensions [9]. Finally, they used ANFIS for prediction of how five parameters can effect on outputs the ANFIS network was performed to determine how the five parameters affect the wake wind speed [10]. In another article they adapted to estimate wind farm efficiency according to turbines number in wind farm [11]. Furthermore, Khademi et al., applied ANN, ANFIS and regression for prediction of strength of recycled aggregate concrete [12]. They are concluded that ANN and ANFIS are better in mix design optimization and in the case of higher accuracy requirements. After that, they used same models for prediction of 28 days compressive strength of concrete [13]. The results were similar in the case of using these models, when higher accuracy is needed, the ANN and ANFIS models are proposed.
ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM
Artificial neural network which can be identified as the data processing systems, are algorithms simulating the functioning of the biologic neurons. An Adaptive Neuro-Fuzzy Inference System (ANFIS) is a hybrid predictive model which uses both of neural network and fuzzy logic to generate mapping relationship between inputs and outputs [6]. The structure of this model consists of five layers in which each layer is constructed by several nodes. As in a neural network, in an ANFIS structure the inputs of each layer are gained by the nodes from pervious layer. Figure 1b describes an ANFIS structure. It can be inferred from figure 1b that the network includes m inputs (X1…Xm), which each one consists of n Membership Functions (MFs). Moreover, a layer with R fuzzy rules and also an output layers are contributed to construction of this model. Number of nodes in first layer can be calculated as the product of m as number of inputs and n as number MFs (N=m.n). The number of nodes in other layers (layer 2-4) relates to number of fuzzy rules (R).The layers of an ANFIS model can be summarized as follows:
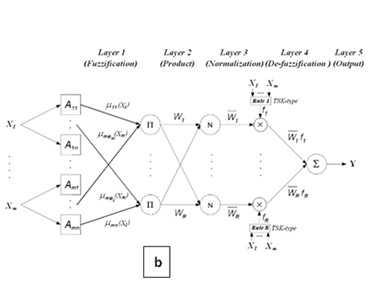
Figure 2: Structure of adaptive neuro-fuzzy inference system graphene is a monoatomic layer of carbon atoms in a honeycomb lattice [1,6]. It is one of the strongest materials ever used with tensile strengths over 130 GP making it 200 times as strong as steel [14].The unique chemical structure of Graphene has been attractive for biologists and biomedical properties [15].
First layer: Fuzzification layer
In this layer crisp inputs transforms to linguistic type Aij (such as bad, middle, good) by using membership functions. The output of this layer can be expressed as:
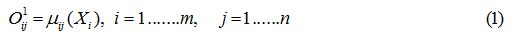
Where μij is the jth membership function for the input Xi. Several types of MFs are used, for example, triangular, trapezoidal and generalized bell function. In this study, the Triangular and Gaussian functions were selected for ultimate tensile strength and elongation respectively. The mathematical equations for Triangular and Gaussian type of membership function are expressed as equations 2 and 3 respectively:
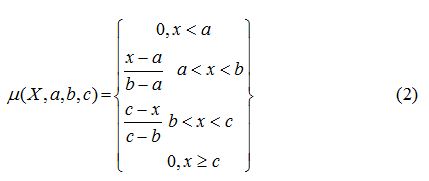
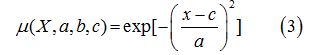
Where a and b vary the width of the curve and c locates the center of the curve. The parameter b should be positive. These parameters are named as premise parameters.
Second layer: Product layer
Third layer: Normalized layer
Fourth layer: Defuzzification
Fifth layer: Output layer (for further details refer to reference 4)
The Root Mean Square Error (RMSE) function is applied to this network for inspection of trained model performances. It can be calculated by following equation:
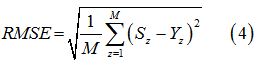
Where, M is the total number of training sample, Sz is the real output value, and Yz is the ANFIS output value in training [6].
In order to correlate the relationship between input parameters and responses, this model has been employed. The first step is to identify the input (e.g., laser power, powder feeding rate, carrier gas flow rate, etc). And output (e.g., catchment efficiency and clad height or weight) parameters of the process. These parameters can be either quantitative or qualitative depending on the research objectives. To this end, researchers rely on either experimental or simulation works (or a combination of both) to optimize the laser cladding process.
Laser cladding has a great potential to benefit these cutting-edge technologies, as laser deposition techniques can provide a revolutionary technique for making micro structure fabrication. Optomec Inc., is a company in the USA, has advanced a new process for making micro coating on substrates which is in the range of 10 to 50μm.
The laser cladding process has drawn great attention both from researchers and users. Consequently with the advent of artificial intelligent system especially ANFIS. We strongly believe that optimizing the laser cladding process for hybrid alloys of graphene/metallic material will significantly improve the characterization of response parameters. Moreover, ANFIS model can be applied to generate mapping relationship between process factors and responses. Also, it will estimate the output parameters with maximum accuracy. In other words, the main advantages of the ANFIS scheme are: computationally efficient, well-adaptable with optimization and adaptive techniques. To use the effect of input parameters on the outputs, MATLAB (ANFIS toolbox) can be used. Furthermore, the effect of process factors (processing inputs) on the outputs can be studied through plots derived out of models developed in ANFIS simulation.

Figure 2: Structure of adaptive neuro-fuzzy inference system graphene is a monoatomic layer of carbon atoms in a honeycomb lattice [1,6]. It is one of the strongest materials ever used with tensile strengths over 130 GP making it 200 times as strong as steel [14].The unique chemical structure of Graphene has been attractive for biologists and biomedical properties [15].
First layer: Fuzzification layer
In this layer crisp inputs transforms to linguistic type Aij (such as bad, middle, good) by using membership functions. The output of this layer can be expressed as:
Where μij is the jth membership function for the input Xi. Several types of MFs are used, for example, triangular, trapezoidal and generalized bell function. In this study, the Triangular and Gaussian functions were selected for ultimate tensile strength and elongation respectively. The mathematical equations for Triangular and Gaussian type of membership function are expressed as equations 2 and 3 respectively:
Where a and b vary the width of the curve and c locates the center of the curve. The parameter b should be positive. These parameters are named as premise parameters.
Second layer: Product layer
Third layer: Normalized layer
Fourth layer: Defuzzification
Fifth layer: Output layer (for further details refer to reference 4)
The Root Mean Square Error (RMSE) function is applied to this network for inspection of trained model performances. It can be calculated by following equation:
Where, M is the total number of training sample, Sz is the real output value, and Yz is the ANFIS output value in training [6].
In order to correlate the relationship between input parameters and responses, this model has been employed. The first step is to identify the input (e.g., laser power, powder feeding rate, carrier gas flow rate, etc). And output (e.g., catchment efficiency and clad height or weight) parameters of the process. These parameters can be either quantitative or qualitative depending on the research objectives. To this end, researchers rely on either experimental or simulation works (or a combination of both) to optimize the laser cladding process.
Laser cladding has a great potential to benefit these cutting-edge technologies, as laser deposition techniques can provide a revolutionary technique for making micro structure fabrication. Optomec Inc., is a company in the USA, has advanced a new process for making micro coating on substrates which is in the range of 10 to 50μm.
The laser cladding process has drawn great attention both from researchers and users. Consequently with the advent of artificial intelligent system especially ANFIS. We strongly believe that optimizing the laser cladding process for hybrid alloys of graphene/metallic material will significantly improve the characterization of response parameters. Moreover, ANFIS model can be applied to generate mapping relationship between process factors and responses. Also, it will estimate the output parameters with maximum accuracy. In other words, the main advantages of the ANFIS scheme are: computationally efficient, well-adaptable with optimization and adaptive techniques. To use the effect of input parameters on the outputs, MATLAB (ANFIS toolbox) can be used. Furthermore, the effect of process factors (processing inputs) on the outputs can be studied through plots derived out of models developed in ANFIS simulation.
REFERENCES
- Toyserkani E, Khajepour A, Corbin SF (2004) Laser cladding. CRC press,Taylor & Francis Group, England, London.
- Oliveira U, Ocelik V, Hosson J (2005) Analysis of coaxial laser cladding processing conditions. Surface and Coating Technology 197: 127-136.
- Weisheit A, Backes G, Stromeyer R, Gasser A, Wissenbach K, et al. (2001) Powder Injection: The Key to Reconditioning and Generating Components Using Laser Cladding. Proceedings of International Congress on Advanced Materials and Processes, Materials Week 2001, Munich, Germany.
- Sohrabpoor H (2016) Analysis of laser powder deposition parameters: ANFIS modeling and ICA optimization. Optik - International Journal for Light and Electron Optics 127: 4031-4038.
- Wang Y, Li Z, Wang J, Li J, Lin Y (2011) Graphene and graphene oxide: biofunctionalization and applications in biotechnology. Trends Biotechnol 29: 205-212.
- Liu Z, Robinson JT, Tabakman SM, Yang K, Dai H (2011) Carbon materials for drug delivery and cancer therapy. Materials Today 14: 316-323.
- Babar IM, Harun SW, Yasin M, Ahmada H (2017) Mode-locking pulse generation in cladding pumped Erbium-Ytterbium co-doped fiber laser with graphene PVA film. Optik - International Journal for Light and Electron Optics 136: 531-535.
- Liu Y, Qu W, Su Y (2016) Tic Reinforcement Composite Coating Produced Using Graphite of the Cast Iron by Laser Cladding. Materials (Basel) 9: 815.
- Petkovic D, Nikolic V, Mitic VV, Kocic LM (2017) Estimation of fractal representation of wind speed fluctuation by artificial neural network with different training algorithms. Flow Measurement and Instrumentation 54: 172-176.
- Petkovic D, Cojbašic Z, Nikolic V (2013) Adaptive neuro-fuzzy approach for wind turbine power coefficient estimation. Renewable and Sustainable Energy Reviews 28: 191-195.
- Nikolic V, Mitic VV, Kocic L, Petkovic D (2017) Wind speed parameters sensitivity analysis based on fractals and neuro-fuzzy selection technique. Knowledge and Information Systems 52: 255-265.
- Petkovic D, Hamid SHA, Cojbašic Z, Pavlovic NT (2014) Adapting project management method and ANFIS strategy for variables selection and analyzing wind turbine wake effect. Natural Hazards 74: 463-475.
- Petkovic D, Pavlovic NT, Cojbašic Z (2016) Wind farm efficiency by adaptive neuro-fuzzy strategy. International Journal of Electrical Power & Energy Systems 81: 215-221.
- Khademi F, Jamal SM, Deshpande N, Londhe S (2016) Predicting strength of recycled aggregate concrete using Artificial Neural Network, Adaptive Neuro-Fuzzy Inference System and Multiple Linear Regression. International Journal of Sustainable Built Environment 5: 355-369.
- Khademi F, Akbari M, Jamal SM, Nikoo M (2017) Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Frontiers of Structural and Civil Engineering 11: 90-99.
Citation: Sohrabpoor H (2017) Perspective of Applying Adaptive Neuro Fuzzy Inference System (ANFIS) in Laser Cladding of Graphene-Metal Alloys. J Nanotechnol Nanomed Nanobiotechnol 4: 017.
Copyright: © 2017 Hamed Sohrabpoor, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Journal Highlights
© 2024, Copyrights Herald Scholarly Open Access. All Rights Reserved!
