
A Finite Element Analysis of Wire Diameter, Material, and Applied Force Interaction in K-Wire Fixation Stresses
*Corresponding Author(s):
Matthew BA McCulloughDepartment Of Chemical Biological And Bioengineering, North Carolina Agricultural And Technical State University, North Carolina , United States
Tel:336 334 7904,
Email:mattbm@ncat.edu
Abstract
Background: K-wire fixation is popular procedure for digital replantation. Though successful, complications can occur, which may be attributed to improper mechanical interactions.
Methods: Simplified models of a bone-wire systems simulated stress based on varying applied forces (100N or 200N), materials (Nitinol or Poly Lactic Acid (PLA)) and wire diameters (1.25mm or 2.4mm). Material properties were assumed to be isotropic and homogeneous. Statistical tests were used to investigate the interaction and main effects of these factors and whether they are significant in this study, with α=0.05.
Results: Von Mises stresses observed from the various treatments were shown to have no interaction with each other, having to reject the alternative hypothesis with all interactions resulting in P values greater than 0.05. However, the only factor significantly impacting Von Mises stress was the diameter of the wire.
Keywords
INTRODUCTION
Digital replantation has been a well-established technique for reconstructive hand surgery since the late 1960’s. Completely severed digits can be reattached, often leading to regained functionality [1,2]. A key aspect of these replantation surgeries is the fixation method. Several fixation techniques exist to immobilize the digit during the healing process, supporting contact long enough for soft tissues, blood vessels, and bone remodeling to occur [3,4]. Although relatively successful, post-operative complications can occur. Unfortunately, patients can experience the loss of 40-50% of their hand function, depending on the injury and chosen fixation method [5]. Success rates can be hindered by the occurrence of nonunion/malunion, or stiffness in the replanted digit, leading to reoperation in severe cases [6].
Many fixation methods involve Kirschner wires, plates, and screws. Finite Element Analysis methods have been employed to explore complications of K-wire fixation [7,8]. Meng et al., compared wire displacement values for mini external fixation and internal fixation used in the treatment of Bennet fractures [9]. The case involved a healthy male with no disease. 3D digital models of the first and second metacarpal bones, and trapezium were created via CT. A 100N load was applied to the mini external fixator, assuming homogeneous, isotropic and continuous material properties. The results of the study showed that external fixation as a more effective fixation method compared to internal methods. Zamani et al., theoretically and computationally examined the use of k-wires in an Ilizarov external fixator, to evaluate the lateral deflection [10]. In this study, bone was simplified to a hollow cylinder, and the wire-bone interaction was assumed frictionless. In spite of these simplifications, FEA results were similar to mathematical predictions for deflection and tension in the k-wires. This study highlights the validity and potential impact of high fidelity models of k-wire-bone interactions. In spite of the promise of the technology, limited studies exist that explore the impact of design parameters on k-wire performance. Therefore, the purpose of this study was to investigate the statistical interactions between k-wire diameter, material, and applied force during digital fixation.
METHODS
Solidworks (Dassault Systemes, 2017) 3D modeling and analysis software was used. A simplified geometry was used that included both a k-wire and bone analog, in the form of cylinders. The bone cylinder (an extruded circle) had a diameter of 2cm the approximate average width of a human finger, 2cm [11], and a cylindrical hole through the center as a space for the k wire. Two cylinders with hole diameters of 1.25mm and 2.4mm were created based on known k-wire diameters used in practice and on the market. Bone cylinders were assigned custom material properties based on values of cortical bone, from Currey et al., as the phalanges have a higher proportion of cortical bone [12, 13]. The k-wire was modeled as a narrow cylinder extruded from a circle with matching diameters to those of the holes in the bone cylinders, and assigned material properties of either Nitinol (Titanium-Nickel alloy) [14] or Polylactic Acid (PLA, a bioresorbable polymer) [15], as both are materials used for k-wires. The wires were assumed to be isotropic and homogeneous. In each simulation, bone and wire were brought together in an assembly file, where the inner surface of the hole in the bone was mated with the face of the k wire cylinder. A contact pair was determined by allowing the software to automatically determine the contact locations between parts. The surfaces were assumed to be bonded, and the friction coefficient was left at a default of 0.5. Both the bone and K wire were meshed with 10-noded parabolic tetrahedral elements, after selecting the option for a “high quality” mesh. An h-adaptive mesh convergence study was conducted. Such an analysis automatically refines the mesh by reducing the size of each element and increasing the number of elements in the model, until a target accuracy is achieved. This target accuracy is an evaluation of the difference in output between mesh iterations. For this analysis, target accuracy in von Mises stress was set to 90%. Therefore a difference of 10% or less in von Mises stresses between mesh iterations meant the model was converged. The final model was composed of 845,560 nodes, 620,928 elements, and 2,530,302 Degrees of Freedom (DOF). The final accuracy of the model was 20%, which did not meet the original target of 10% (Table 1 & Figure 1).
|
|
Cortical Bone |
Nitinol |
Polylactic Acid (PLA) |
|
Elastic Modulus |
17 GPa |
83 MPa |
3.5 GPa |
|
Poisson’s Ratio |
0.33 |
0.33 |
0.36 |
|
Tensile Strength |
148 MPa |
895 MPa |
50 MPa |
|
Yield Strength |
135 MPa |
195 MPa |
60 MPa |
Table 1: Material Properties Chosen for Bone and K-Wire Modeling.
 Figure 1: (left) K-wire and bone system in SolidWorks (right) Identified contact set for bonded surfaces.
Figure 1: (left) K-wire and bone system in SolidWorks (right) Identified contact set for bonded surfaces.
Boundary conditions included eliminating motion on the outer surface of the bone cylinder, except for the top surface, thus eliminating the ability of the bone cylinder to move. Such a boundary condition may be considered an over-constraint. However this simulation represented an in vitro or benchtop examination of k-wire behavior. Therefore such a constraint is needed to replicate bench top experiments. The proximal end of the wire (i.e., the face opposite to the applied force) was fixed, while the distal end remained unbound. A distributed, axial force of either 100N or 200N was applied to the free end of the wire to represent compression acting across finger joints during manual tasks. While k-wires experience tensile and compressive loads, this preliminary analysis focused on compression only, as it is a key component in healing. Von Mises stresses were reported from a single node on the top edge of the wire (Figure 2).
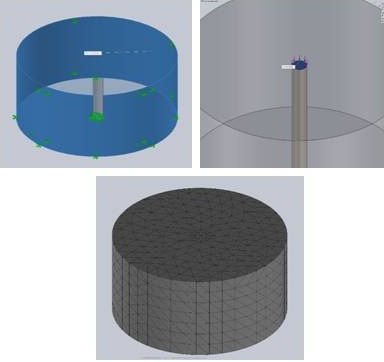 Figure 2: (a) Fixed geometries are defined with all sides of the bone except the top (b) a 100N Load is applied to the distal end of the wire (c) the bone-wire assembly is meshed and ready to run with all parameters assigned.
Figure 2: (a) Fixed geometries are defined with all sides of the bone except the top (b) a 100N Load is applied to the distal end of the wire (c) the bone-wire assembly is meshed and ready to run with all parameters assigned.
To determine the treatments to test, a 2k factorial design was created with diameter, material, and applied force as three independent variables, each with two levels, and Von Mises Stress as the dependent variable (observed). Eight unique treatments were determined to be tested based on this design (Tables 2 & 3).
|
Factor |
Factor Defined |
+ |
- |
|
A |
Diameter |
2.4mm |
1.25mm |
|
B |
Material |
Nitinol |
PLA |
|
C |
Applied Force |
200N |
100N |
|
Treatment |
Diameter |
Material |
Force |
|
a |
2.4mm |
PLA |
100N |
|
b |
1.25mm |
Nitinol |
100N |
|
c |
1.25mm |
PLA |
200N |
|
ab |
2.4mm |
Nitinol |
100N |
|
ac |
2.4mm |
PLA |
200N |
|
bc |
1.25mm |
Nitinol |
200N |
|
abc |
2.4mm |
Nitinol |
200N |
|
-1 |
1.25mm |
PLA |
100N |
Table 3: Treatment assignments based on 23 factorial design.
The data was analyzed via SAS 9.4 software to view residual plots for normality and homogeneity assumptions to ensure no violations were found, along with ANOVA results with α=0.05. Interaction effects and simple main effects were also calculated. Residual plots support the assumptions of normality and homogeneity within the data set. Observations were blocked according to the diameter level, as this parameter impacted statistical plots. This choice is further supported by the p value of <0.05, for the blocked factor in table 5, rejecting the null hypothesis that there is no difference with the blocked factor included in the data set.
RESULTS
The results of the simulation and statistical analysis showed that the diameter of the k wire has a significant effect on the stresses observed, yielding the highest effect. In addition, the interaction effect of the diameter and applied force onto the wire was considerably high. The interaction effects between the force applied to the wire and the diameter of the wire were large in comparison to the effects between the material and diameter (Figures 3 & 4; Tables 4-7).
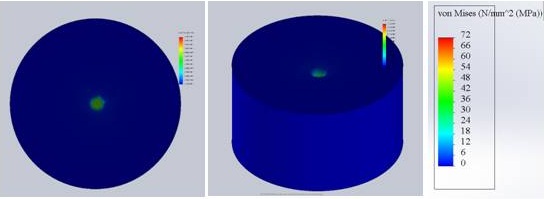 Figure 3: (a) Nitinol wire results from a top and side view with Von Mises stress gradient for 200N and 1.25mm wire (bottom left/right) PLA wire results from a top and side view with Von Mises stress gradient.
Figure 3: (a) Nitinol wire results from a top and side view with Von Mises stress gradient for 200N and 1.25mm wire (bottom left/right) PLA wire results from a top and side view with Von Mises stress gradient.
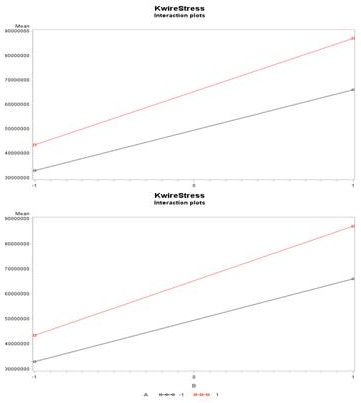 Figure 4: Interaction plots show (a) load having no effect on the relationship between von Mises stress and the selected material. The red line represents a 200N load while the black line represenets a 100N load. The “-1” designation along the x-axis represents the material PLA, while the “+1” represents Nitinol. The Y-axis is the average von Mises stress in Pa for the simulation.; and (b) the selected material having no effect on the relationship between von Mises stress and applied Force. The red line represents Nitinol while the black line represenets PLA. The “-1” designation along the x-axis represents a 100N load, while the “+1” represents a 200N load. The Y-axis is the average von Mises stress in Pa for the simulation. As the lines do not intersect in either plot, it is believed to be no effect of these categorical variables on each other.
Figure 4: Interaction plots show (a) load having no effect on the relationship between von Mises stress and the selected material. The red line represents a 200N load while the black line represenets a 100N load. The “-1” designation along the x-axis represents the material PLA, while the “+1” represents Nitinol. The Y-axis is the average von Mises stress in Pa for the simulation.; and (b) the selected material having no effect on the relationship between von Mises stress and applied Force. The red line represents Nitinol while the black line represenets PLA. The “-1” designation along the x-axis represents a 100N load, while the “+1” represents a 200N load. The Y-axis is the average von Mises stress in Pa for the simulation. As the lines do not intersect in either plot, it is believed to be no effect of these categorical variables on each other.
|
Treatment |
A |
B |
C |
AB |
AC |
BC |
ABC |
Obs |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Von Mises Stress in MPa) |
|
-1 |
- |
- |
- |
+ |
+ |
+ |
- |
51000000 |
|
a |
+ |
- |
- |
- |
- |
+ |
+ |
15100000 |
|
b |
- |
+ |
- |
- |
+ |
- |
+ |
66000000 |
|
c |
- |
- |
+ |
+ |
- |
- |
+ |
102000000 |
|
ab |
+ |
+ |
- |
+ |
- |
- |
- |
21100000 |
|
ac |
+ |
- |
+ |
- |
+ |
- |
- |
30200000 |
|
bc |
- |
+ |
+ |
- |
- |
+ |
- |
132000000 |
|
abc |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
42300000 |
Table 4: 23 factorial design and observed Von Mises Stress Results for each treatment.
|
Source |
DF |
Type III SS |
Mean Square |
F Value |
Pr> F |
|
B |
1 |
5.01E+14 |
5E+14 |
1.64 |
0.2907 |
|
C |
1 |
2.93E+15 |
2.9E+15 |
9.6 |
0.0534 |
|
B*C |
1 |
5.56E+13 |
5.6E+13 |
0.18 |
0.6985 |
|
block |
1 |
7.34E+15 |
7.3E+15 |
24 |
0.0163 |
Table 5: SAS calculated ANOVA results for factors B and C with factor A levels as blocks.
|
Main Effect A= |
-6.06E+07 MPa |
|
Main Effect B= |
1.58E+07 MPa |
|
Main Effect C= |
3.83E+07 MPa |
|
Interaction Effect AB= |
-6.77E+06 MPa |
|
Interaction Effect AC= |
-2.02E+07 MPa |
|
Interaction Effect BC= |
5.27E+06 MPa |
|
Interaction Effect ABC= |
-2.26E+06 MPa |
Table 6: Calculated main effect and interaction effect values for all factors.
|
Test for Normality |
||||
|
Test |
Statistic |
p Values |
||
|
Shapiro-Wilk |
w |
0.908529 |
Pr < W |
0.3438 |
|
Kolmogorov-Smirnov |
D |
0.187198 |
Pr > D |
>0.1500 |
|
Cramer-von Mises |
w-Sq |
0.057597 |
Pr > W-Sq |
>0.2500 |
|
Anderson-Darling |
A-Sq |
0.34231025 |
Pr > A-SQ |
>0.2500 |
Table 7: SAS Generated test for Normality (Specifically Shapiro-Wilk P value).
The resulting Von Mises stresses, compared across conditions, were shown to not be significantly different, leading us to reject the alternative hypothesis (all interactions resulted in values for p>0.05). The only significantly different stress outcomes, resulted from changes to the wire diameter as seen in the main effect results.
DISCUSSION
The purpose of this study was to investigate the potential interactions between designs parameters, of k-wires used for replantation. Initial results show the wire diameter having the greatest influence on von Mises stresses. Limitations of this work include simplifications of the geometry of the bone and wire as well as loading conditions. The simplified shapes failed to consider the full length nor taper the wire and any subsequent stress transmission properties of the wire. In addition, the material properties of the bone were assumed homogeneous and isotropic while bone is considered an anisotropic material that also exhibits viscoelastic behaviors. Other soft tissues were not included in the model, and may impact these results [16]. The loading and boundary conditions were also simplified; a singular loading direction was used. In practice, forces act in multiple directions on the wire and bone. Limited visibilities of the von Mises stresses indicate that the magnitude of the load may not have been sufficient to create a statistical difference. Future work development the model and include a validation study, via physical experimentation. Additional components should be built into the model, such as soft tissues, and vasculature which play key roles in healing. It is also important to note that additional statistical tests of other factors modeled must be ran, in order to better understand the interactions between the various factors.
CONCLUSION
Many non-surgical factors statistically impact the outcome of replantation post operatively. Accuracy of k-wire modeling is impacted by vasculature, and soft tissue interactions which impact the healing process. Many models ignore these factors requiring more complex model development. The work presented was a preliminary evaluation of the statistical interactions of various design parameters associated with k-wire fixation. It was concluded that little to no interactions between the designs parameters studied. Such findings suggest the additional importance of procedural technique, in the success of these procedures.
CONFLICT OF INTEREST
The author of this paper has no financial or personal relationships with other people or organizations that could inappropriately influence (bias) the study.
ACKNOWLEDGEMENTS
This work was supported with funding from North Carolina A&T State University and the department of Chemical, Biological, and Bioengineering. The authors would also like to thank Mr. Emmanuel Tetteh for his consultation regarding computational modeling.
REFERENCES
- Fujioka M, Hayashida K (2015) Proximal interphalangeal replantation with arthrodesis facilitates favorable esthetics and functional outcome. J Trauma Manag Outcomes 9: 7.
- Woo SH, Kim YW, Cheon HJ, Nam HJ, Kang DH, et al. (2015) Management of Complications Relating to Finger Amputation and Replantation. Hand Clin 31: 319-338.
- Sud V, Freeland AE (2002) Skeletal fixation in digital replantation. Microsurgery 22: 165-171.
- Vu?eti? ?, Vukašinovi? Z, Manojlovi? R, Tuli? G, Vu?kovi? ?, et al. (2014) Evaluation of reversal osteofixation using K-wires in digital replantation . Srp Arh Celok Lek 142: 34-39.
- Neinstein R, Linda T Dvali, Suzanne Le, Anastakis DJ (2012) Complete digital amputations undergoing replantation surgery: A 10-year retrospective study. Hand (N Y) 7: 263-266.
- Ezerins SA, Harm CJ, Kempton SJ, Salyapongse AN (2014) Rehabilitation Following Replantation in the Upper Extremity. Extremity Replantation 191-206.
- Lee SW, Lee DC, Kim JS, Roh SY, Lee KJ (2017) Analysis of Bone Fixation Methods in Digital Replantation. Arch Plast Surg 44: 53-58.
- Cheng H-S, Wong L-Y, Chiang I, Chan I, Yip T-H, et al. (2004) Comparison Of Methods Of Skeletal Fixation For Severely Injured Digits. Hand Surgery 9: 63-69.
- Meng L, Zhang Y, Lu Y (2013) Three-dimensional finite element analysis of mini-external fixation and Kirschner wire internal fixation in Bennett fracture treatment. Orthop Traumatol Surg Res 99: 21-29.
- Zamani AR, Oyadiji SO (2010) Theoretical and Finite Element Modeling of Fine Kirschner Wires in Ilizarov External Fixator. J Med Devices 4: 031001.
- Dandekar K, Raju BI, Srinivasan MA (2003) 3-D Finite-Element Models of Human and Monkey Fingertips to Investigate the Mechanics of Tactile Sense. J Biomech Eng 125: 682-691.
- Currey JD (1984) The mechanical adaptations of bones. Princeton University Press, Princeton, New Jersey, USA.
- Mays S (2010) The archaeology of human bones. Routledge, London, United Kingdom.
- http://jmmedical.com/resources/221/Nitinol-Technical-Properties.html
- https://www.makeitfrom.com/material-properties/Polylactic-Acid-PLA-Polylactide
- Rogge RD, Adams BD, Goel VK (2002) An analysis of bone stresses and fixation stability using a finite element model of simulated distal radius fractures. J Hand Surg Am 27: 86-92.
Citation: Nelson T, McCullough MBA (2018) Myeloid A Finite Element Analysis of Wire Diameter, Material, and Applied Force Interaction in K-Wire Fixation Stresses. Curr Trends Med Bio Eng 1: 001.
Copyright: © 2018 Trevon Nelson, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

