
Journal of Nanotechnology Nanomedicine & Nanobiotechnology Category: Medical
Type: Research Article
Ab Initio Study of Azomethine Derivative Cancer Drug on Boron Nitride and Graphene Nanoflakes
*Corresponding Author(s):
Fabien PicaudFemto St, Université Bourgogne Franche-Comté, 15 Bis Avenue Des Montboucons, 25030 Besancon, France
Tel:+003 3381666284,
Fax:003 3381666275
Email:fabien.picaud@univ-fcomte.fr
Received Date: Mar 20, 2017
Accepted Date: Apr 26, 2017
Published Date: May 16, 2017
Abstract
One of the main steps to realize targeted treatment is to build up effective target drug delivery nanosystems. Herein we present theoretical results, based on density functional theory, which demonstrate the potentiality of functionalization of perfect 2D nanomaterials (i.e., graphene and boron nitride nanoflakes) with anticancer molecule. Our first observations have confirmed that a perfect nanoflake blocked any chemical reaction onto them and could only transport physically active drug. Moreover, on defective surface, the resulting chemical attachment of an azomethine plus subsequent drug (like an anticancer Pt(IV) complex as cisplatin molecule) onto these materials via a cycloaddition process show the formation of a five membered ring. Moreover, the electronic activity and the structure of the drug are conserved in the most stable configuration, which means that the drug could delivered through this platform according to a supplementary target ligand.
Keywords
DFT calculations; Graphene: boronene; Nanoflakes; Therapeutic agents
INTRODUCTION
The use of nanotechnology to improve the efficacy of anticancer treatment was mainly focused in the targeting drug delivery field. Various types of drug/agent nanovectors were prepared including quantum dots, dendrimers, Carbon Nanotubes (CNTs), gold and silver nanoparticles, liposomes and micelles [1-6].
Amongst all these nanomaterials a small number were commercialized and very few are in clinical studies [7]. Ideally, any new class of drug carriers must fulfill several criteria: efficient drug transport and targeting, successful drug release at specific location. Recently some theoretical calculations were dedicated to study the structure, the properties and the stability of some new class of drug nanovectors [8-10]. Some very promising results were obtained showing the possibility of achieving anticancer drug transport (anticancer agent (Pt(IV)) complexes linked to an amino-derivative chain) thanks to CNT as well as to Boron Nitride Nanotubes (BNNT). The most stable physisorption state was localized inside the nanotube in the case of BNNT. The molecular chemisorption was located on the outer surface of the nanovector (between two carbon atoms of a same hexagon for CNT, and above two adjacent B and N atoms for BNNT hexagon only) with no perturbation of the cycloaddition process in all cases [11,12].
Despite these tubular geometries new nanostructures are now in development for future applications in medicine. Among them, Ciesielski et al., demonstrated the exfoliation of many different 2D structures such as graphene and boron nitride with high up to scale production [13]. Due to their exceptional surface area 2D nanomaterials can be envisioned as promising drug delivery systems. In this paper we report some new theoretical results concerning the adsorption of anticancer agent (Pt(IV)) complexes linked to an amino-derivative chain molecule on graphene and boron nitride 2D surface (nanoflake). Thanks to full atom Density Functional Theory (DFT) calculations, we investigate the energy behavior of the anticancer molecule interacting with the 2D nanoflakes. We demonstrate that the molecule can be grafted spontaneously onto these nanostructures. To prove this, we investigated the energy stability of the functionalized systems through the changes of their morphology and their electronic structure thanks to Partial Density of States (PDOS) and Bader charge analysis. The conditions for physisorption and chemisorption of the anticancer drug molecule will be given, opening the route for developing ultimate 2D targeting systems, if specific ligand would be added to the vector.
Amongst all these nanomaterials a small number were commercialized and very few are in clinical studies [7]. Ideally, any new class of drug carriers must fulfill several criteria: efficient drug transport and targeting, successful drug release at specific location. Recently some theoretical calculations were dedicated to study the structure, the properties and the stability of some new class of drug nanovectors [8-10]. Some very promising results were obtained showing the possibility of achieving anticancer drug transport (anticancer agent (Pt(IV)) complexes linked to an amino-derivative chain) thanks to CNT as well as to Boron Nitride Nanotubes (BNNT). The most stable physisorption state was localized inside the nanotube in the case of BNNT. The molecular chemisorption was located on the outer surface of the nanovector (between two carbon atoms of a same hexagon for CNT, and above two adjacent B and N atoms for BNNT hexagon only) with no perturbation of the cycloaddition process in all cases [11,12].
Despite these tubular geometries new nanostructures are now in development for future applications in medicine. Among them, Ciesielski et al., demonstrated the exfoliation of many different 2D structures such as graphene and boron nitride with high up to scale production [13]. Due to their exceptional surface area 2D nanomaterials can be envisioned as promising drug delivery systems. In this paper we report some new theoretical results concerning the adsorption of anticancer agent (Pt(IV)) complexes linked to an amino-derivative chain molecule on graphene and boron nitride 2D surface (nanoflake). Thanks to full atom Density Functional Theory (DFT) calculations, we investigate the energy behavior of the anticancer molecule interacting with the 2D nanoflakes. We demonstrate that the molecule can be grafted spontaneously onto these nanostructures. To prove this, we investigated the energy stability of the functionalized systems through the changes of their morphology and their electronic structure thanks to Partial Density of States (PDOS) and Bader charge analysis. The conditions for physisorption and chemisorption of the anticancer drug molecule will be given, opening the route for developing ultimate 2D targeting systems, if specific ligand would be added to the vector.
METHODS
The adsorption of azomethine + anticancer Pt(IV) drug complex (AzPt) onto the surfaces of Graphene (GRN) and Boron Nitride (BNN) nanoflakes was considered using the SIESTA suite of program i.e. using periodic Kohn-Sham DFT calculations [14,15]. We used the Perdew–Burke–Ernzerhof (PBE) Generalized Gradient Approximation (GGA) for the exchange correlation density functional as implemented in the SIESTA package to determine the total energies [16,17]. All calculations were performed without spin polarization. We used the self-consistency mixing rate of 0.1, a maximum force tolerance of 0.02eV.Å-1 and a mesh cut off of 100 Ry (the variations of these parameters showed a very low perturbation of the total adsorption energies by less than 0.2%, i.e. at most 9x10-3 eV for cut off of 350 Ry). The self-consistent cycles were stopped when variations of the total energy per unit cell and band structure energy were both less than 10-4 eV.
The 2D nanoflakes envisioned and AzPt molecules were studied using the same unit cell (i.e. 60x60x60 Å3) as depicted in figure 1. Note that the cisplatin form was not considered because this form is less stable in vacuum than the transplatin one, due to strong Cl/Cl repulsion. Note also that the great interest to use an amino-derivative chain is to have a spacer permitting to pull the anticancer molecule away from the nanovector and let the system forming chemical bonding facilities. Given the large unit cell, the Brillouin zone was sampled using a single k-point at the center Γ. We studied different nanoflake systems with or without atom defect. The calculated average C–C (B-N) bond lengths for graphene and boron nitride nanoflakes were 1.42 Å and 1.44 Å, respectively. The GRN lateral size was 22.80x25.25 Å2 that corresponded to 180 C atoms when perfect GRN was simulated (or 179 C atoms when one atom defect was considered) plus 38 H atoms to avoid boundary effects at the dangling bonds. For BNN, the lateral size was 25.78x23.34 Å2 and 90 B, 90 N and 38 H atoms (to avoid, as aforementioned, boundary effects) were necessary. To consider defective BNN, two cases were envisaged (the first (second) one was built with one B (N) atom defect).
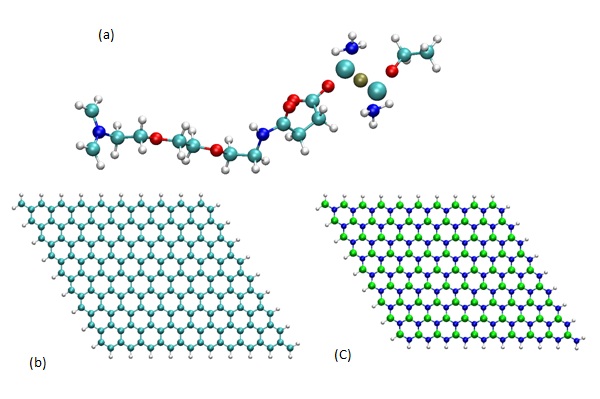
Figure 1: Geometry of (a) AzPt molecule, (b) GRN with H termination, (c) BNN with H termination (B, N, C, O, H, Pt, and Cl atoms are represented as, green, blue, cyan, red, white, ochre, and large cyan spheres, respectively).
A basis set of localized atomic orbitals (double-ζplus polarization functions), and norm-conserving pseudopotentials were employed.
To understand the nanoflake/drug interactions, the adsorption Energy (Eads) of the adsorbed molecules (AzPt) was defined as: Eads =E(AzPt + nanoflake) - E(nanoflake) - E(AzPt)..
A negative Eads value denotes a more favorable interaction between the drug and the nanoflake surface. In this work, the Van der Waals (VdW) interactions were not taken into account (even if in physisorption case, they could be preponderant) in order to avoid unrealistic parameter calibration in the DFT framework. Moreover, the choice to use periodic type program instead of localized one was motivated by the total atom number in the studied system and the inherent time computations. A detailed comparison of the performance of three different codes, namely i) the Plane Augmented Wave (PAW) approach implemented in VASP, ii) the Full-Potential Linearized Augmented Plane Wave (FP-LAPW) plus local orbital (lo) method implemented in the WIEN2k code and iii) the Gaussian-type orbitals approach, gives similar results for different systems [18-21]. The charge transfers between the nanoflake and the AzPt were analyzed through a partial charge approach (i.e., valence electrons) in the Bader scheme [22-25]. According to this theory, the formation of a bond path is indicated by an accumulation of electron density, ρ(r), between the nuclei of the bonded atoms, which is necessary for bond formation. In this way the path manifests itself in an electron density map through a pair of bonded atoms as a ridge of electron density. Also, the Laplacian of ρ(r)(i.e., ∇2 ρ(r)) marks the boundaries of regions where ρ(r) is locally above or below its average value in the vicinity of r. In the regions where ∇2 ρ(r) is negative, the electronic density is shared by both nuclei (shared interactions). Otherwise, the electrons are concentrated in each of the atomic basins separately and the interaction belongs to the closed-shell type [26,27].
In the simulation, different angular orientations of AzPt were investigated although perpendicular orientation favors the chemical cycloaddition reaction (when possible) as observed on nanotubes [11-12].
The 2D nanoflakes envisioned and AzPt molecules were studied using the same unit cell (i.e. 60x60x60 Å3) as depicted in figure 1. Note that the cisplatin form was not considered because this form is less stable in vacuum than the transplatin one, due to strong Cl/Cl repulsion. Note also that the great interest to use an amino-derivative chain is to have a spacer permitting to pull the anticancer molecule away from the nanovector and let the system forming chemical bonding facilities. Given the large unit cell, the Brillouin zone was sampled using a single k-point at the center Γ. We studied different nanoflake systems with or without atom defect. The calculated average C–C (B-N) bond lengths for graphene and boron nitride nanoflakes were 1.42 Å and 1.44 Å, respectively. The GRN lateral size was 22.80x25.25 Å2 that corresponded to 180 C atoms when perfect GRN was simulated (or 179 C atoms when one atom defect was considered) plus 38 H atoms to avoid boundary effects at the dangling bonds. For BNN, the lateral size was 25.78x23.34 Å2 and 90 B, 90 N and 38 H atoms (to avoid, as aforementioned, boundary effects) were necessary. To consider defective BNN, two cases were envisaged (the first (second) one was built with one B (N) atom defect).

Figure 1: Geometry of (a) AzPt molecule, (b) GRN with H termination, (c) BNN with H termination (B, N, C, O, H, Pt, and Cl atoms are represented as, green, blue, cyan, red, white, ochre, and large cyan spheres, respectively).
A basis set of localized atomic orbitals (double-ζplus polarization functions), and norm-conserving pseudopotentials were employed.
To understand the nanoflake/drug interactions, the adsorption Energy (Eads) of the adsorbed molecules (AzPt) was defined as: Eads =E(AzPt + nanoflake) - E(nanoflake) - E(AzPt)..
A negative Eads value denotes a more favorable interaction between the drug and the nanoflake surface. In this work, the Van der Waals (VdW) interactions were not taken into account (even if in physisorption case, they could be preponderant) in order to avoid unrealistic parameter calibration in the DFT framework. Moreover, the choice to use periodic type program instead of localized one was motivated by the total atom number in the studied system and the inherent time computations. A detailed comparison of the performance of three different codes, namely i) the Plane Augmented Wave (PAW) approach implemented in VASP, ii) the Full-Potential Linearized Augmented Plane Wave (FP-LAPW) plus local orbital (lo) method implemented in the WIEN2k code and iii) the Gaussian-type orbitals approach, gives similar results for different systems [18-21]. The charge transfers between the nanoflake and the AzPt were analyzed through a partial charge approach (i.e., valence electrons) in the Bader scheme [22-25]. According to this theory, the formation of a bond path is indicated by an accumulation of electron density, ρ(r), between the nuclei of the bonded atoms, which is necessary for bond formation. In this way the path manifests itself in an electron density map through a pair of bonded atoms as a ridge of electron density. Also, the Laplacian of ρ(r)(i.e., ∇2 ρ(r)) marks the boundaries of regions where ρ(r) is locally above or below its average value in the vicinity of r. In the regions where ∇2 ρ(r) is negative, the electronic density is shared by both nuclei (shared interactions). Otherwise, the electrons are concentrated in each of the atomic basins separately and the interaction belongs to the closed-shell type [26,27].
In the simulation, different angular orientations of AzPt were investigated although perpendicular orientation favors the chemical cycloaddition reaction (when possible) as observed on nanotubes [11-12].
RESULTS AND DISCUSSION
A-Anticancer drug adsorption onto nanoflakes without defect
The geometry optimization of the AzPt alone (transplatin covalently attached to the amino group) was realized as well as the optimization of the different nanoflakes structure without defect. The total energies for these systems will represent the references in the determination of Eads. Our calculations lead to values equal to -8271.70 eV (i.e., E(AzPt)), -29816.89 eV for the GRN and -35384.69 eV for BNN, respectively (i.e., E(nanoflake)). To study the adsorption interaction, the drug molecule and its carrier were separated by a distance equal to 1.5 Å on the top of two adjacent atoms of one hexagon with an angle AzPt - nanoflake less than 10° or superior to 70°. This distance corresponds nearly to the theoretical distance between bonded atoms in the case of chemisorption of azomethine and carbon nanotube or azomethine and boron nitride nanotube [14,15]. Then the whole structure was relaxed by allowing atoms displacements in the three directions to minimize the total energy (Figure 2).
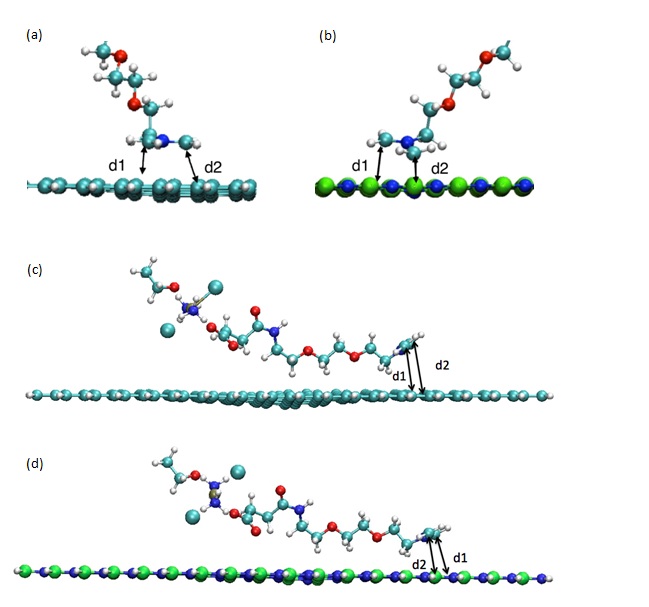
Figure 2: AzPt optimized geometry with angle greater than 70° onto (a) GRN, (b) BNN and AzPt optimized geometry with angle lower than 10° onto (c) GRN, (d) BNN (B, N, C, O, H, Pt, and Cl atoms are represented as green, blue, cyan, red, white, ochre, and large cyan spheres, respectively). d1 and d2 are the distance between C atoms of azomethine and the two adjacent atoms of the nanoflake (i.e., d1(C-C) and d2(C-C) for GRN; d1(C-N) and d2(C-B) for BNN).
By subtracting both the total energy E (nanoflake) of the isolated nanoflake and the energy E(AzPt) of the anticancer molecule from the total energy of the combined structure after optimization, we obtained the binding energy for the interacting systems. The optimized distance between carbon atom of the azomethine (taken as the reference for the interacting system) and atoms of the nanoflake surface was also deduced from the simulations (Table 1).

Figure 2: AzPt optimized geometry with angle greater than 70° onto (a) GRN, (b) BNN and AzPt optimized geometry with angle lower than 10° onto (c) GRN, (d) BNN (B, N, C, O, H, Pt, and Cl atoms are represented as green, blue, cyan, red, white, ochre, and large cyan spheres, respectively). d1 and d2 are the distance between C atoms of azomethine and the two adjacent atoms of the nanoflake (i.e., d1(C-C) and d2(C-C) for GRN; d1(C-N) and d2(C-B) for BNN).
By subtracting both the total energy E (nanoflake) of the isolated nanoflake and the energy E(AzPt) of the anticancer molecule from the total energy of the combined structure after optimization, we obtained the binding energy for the interacting systems. The optimized distance between carbon atom of the azomethine (taken as the reference for the interacting system) and atoms of the nanoflake surface was also deduced from the simulations (Table 1).
| Angle greater than 70° | Angle lower than 10° | |||
| AzPt on GRN | AzPt on BNN | AzPt on GRN | AzPt on BNN | |
| Distance between C atoms of AzPt and atoms of the nanoflake surface | d1(C-C)=3.06 Åd2(C-C)=3.09 Å | d1(C-N)=2.89 Åd2(C-B)=1.83 Å | d1(C-C)=3.72 Åd2(C-C)=3.84 Å | d1(C-N)=3.72 Åd2(C-B)=3.94 Å |
| Eadsorption (eV) | -0.15 eV | -0.22 eV | -0.45 eV | -0.36 eV |
Our results show clearly that the interaction between the anticancer molecule and the two nanoflakes gets attractive while the van der Waals interactions were not taken into account in our approach. The adsorption energy is slightly more stable (i.e., -0.22 eV) in the case of BNN than on GRN (i.e., -0.15 eV) with an angle greater than 70°. On the contrary, when the molecule adsorbed nearly parallel to the surface, the adsorption energy is more stable (i.e., -0.45 eV) on GRN than on BNN (i.e., -0.36 eV). These discrepancies in the adsorption energy can be explained by the resulting distances d1 and d2 and the deformation of the nanoflakes which was more important for GRN than for BNN.
Calculated total electronic Density of States (DOS) (sum of the densities of states for all the atoms in the system) for the optimized positions are represented in figure 3 for nanoflakes alone and AzPt–nanoflake systems with adsorption angle greater than 70°. It is clear that the DOS of AzPt with the nanoflakes structure in figure 3b and figure 3d are almost similar with DOS of GRN and BNN alone, despite some slight discrepancies in the height of DOS and slight shift of energy levels due to interactions with the adsorbate. These DOS modifications could be attributed to the small deformation of the flakes under the specific sites of AzPt adsorption. These deformations could cause an opening of the band gaps at the Fermi level, as recently highlighted in the work of Kundalwal et al., that showed slightly change of the energy levels depending on the geometric constraints applied on the graphene flake [28]. To note the same electronic density of states was obtained for the AzPt-nanoflake system with adsorption angle lower than 10°.
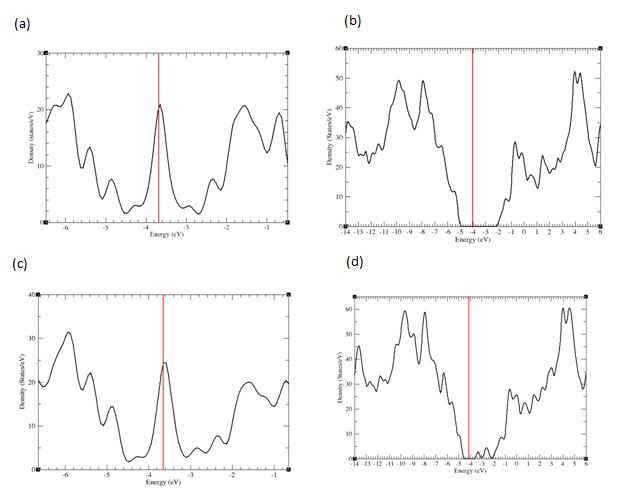
Figure 3: PDOS representation for a) GRN b) AzPt + GRN c) BNN d) AzPt + BNN with AzPt-nanoflake angle greater than 70°.
The Bader charge analysis of the AzPt considered in the gas phase (i.e., 168 e) or adsorbed onto GRN (i.e., 167.9 e) or BNN (i.e., 167.83 e) did not present any significant changes while some small variations onto the Pt and its nearest environment was observed (Table 2).
| Angle greater than 70° | Angle lower than 10° | ||||
| AzPt alone | AzPt on GRN | AzPt on BNN | AzPt on GRN | AzPt on BNN | |
| Pt | 9.30 | 9.30 | 9.27 | 9.32 | 9.29 |
| Cl | 7.237.25 | 7.237.25 | 7.237.24 | 7.227.25 | 7.267.23 |
| NH3 | 7.827.79 | 7.827.80 | 7.857.81 | 7.847.82 | 7.867.81 |
| Total charge | 39.39 | 39.4 | 39.4 | 39.45 | 39.45 |
For adsorption angle greater than 70° (lower than 10°), we observe a slight charge variation on Pt, Cl atoms and NH3 groups with BNN or with GRN in comparison with their charge in the phase gas. However, the overall variation is almost zero (0.01 to 0.06e) when considering the molecular groups surrounding the central Pt atom of AzPt adsorbed on both nanoflakes. We can assume that these small charge variations come from electrostatic interactions between the molecule and the nanoflakes without any chemical functionalization. This would not modify the active behavior of the CisPt molecule.
B-Anticancer drug adsorption onto defective nanoflakes
Among the suitable routes to functionalize nanovectors, cycloaddition reactions are the most straightforward procedure as described in the literature. They lead to favorable heterocyclic five membered rings [29-31]. In order to improve the chemical reactivity of GRN or BNN where no cycloaddition was possible, we have envisioned the creation of one vacancy in the nanosheet centre. In the case of the BNN, two possibilities were considered since the defect could be due to a lack of B or N atom while for GRN only one C atom was moved from the 2D nanosheet to create a vacancy. Then, the energy optimizations of the three defective systems, alone in vacuum, with the aforementioned set of parameters were realized with an adsorption angle greater than 70°. The total energies obtained in these conditions were the references used during the determination of Eads. They were equal to -29646.61 eV for the defective GRN-35270.14 eV for BNN with B vacancy (noted BNN-1) and -35096.78 eV BNN with N vacancy (noted BNN-2). The geometry optimization when the vacancy was introduced in the nanosheets lead to a slight modification of the surface near the defect. Indeed, we can observe that one atom is always off plane whatever the defective surface considered (Figure 4). Its highlights the sp3 localized comportment of the defective surface.
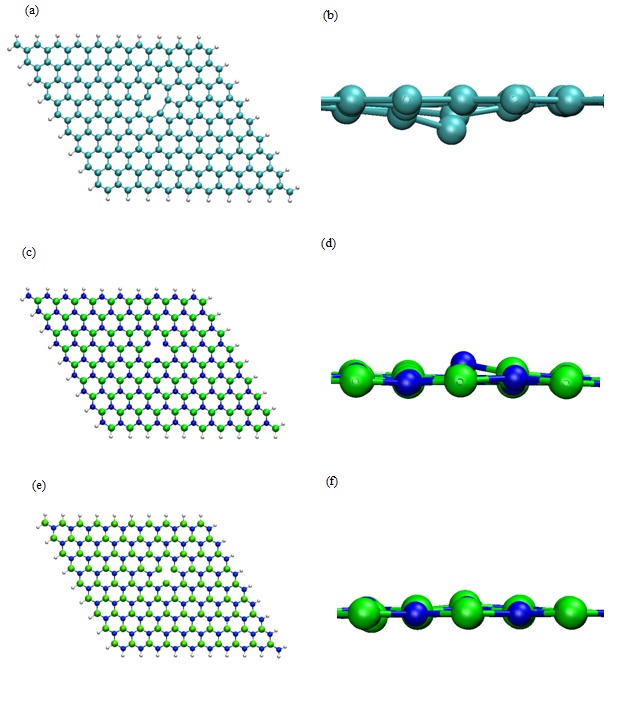
Figure 4: Optimized DFT geometry of (a) Defective GRN with H termination, (b) Lateral zoom in of (a), (c) Defective BNN with H termination (i.e., B defect noted BN-1), (d) Lateral zoom in of (c), (e) Defective BNN with H termination (i.e., N defect noted BN-2) (f) Lateral zoom in of (e). (B, N, C, and H, atoms are represented as green, blue, cyan and white spheres respectively).
Once the defective nanosheets were optimized, we have introduced the anticancer drug near the surface. For each case, the whole system was relaxed in order to minimize the total energy.
In the case of defective GRN two opposite carbon atoms of the same hexagon ring were concerned by the chemical reaction. It leads to a quasi-regular pentagon (Figure 5a). The adsorption energy was low since it reached -3.07 eV for the formation of two C–C bonds with the surface. The distance d1(C1-C2) and d2(C4-C5) were equal to 1.52 Å and 1.58 Å respectively and the angle measured between N3-C2-C1 atoms was equal to 116.71° while it reached 113.02° for the angle formed by N3-C4-C5 atom.
In the case of the BNN-1 a quasi-regular pentagon (Figure 5b) was also obtained with lower adsorption energy equal to -4.45 eV for the formation of two N-C bonds. The distances d1(N1-C2) and d2(C4-N5) were equal to 1.49 Å and 1.52 Å respectively. The angle N3-C2-N1 (N3-C4-N5) was equal to 114.43° (114.70°) as depicted in Figure 5-b. Results obtained in the case of BNN-2 were quite different despite the chemical creation of one pentamer (Figure 5-c). The adsorption energy equal to -2.56 eV for the formation of two B-C bonds was higher than for BNN-1. The distances of adsorption d1(B1-C2) and d2(C4-B5) were also slightly higher since they were equal to 1.65 Å and 1.70 Å, respectively. The analysis of the angle formation lead to values equal to 112.16° (109.11°) for N3-C2-B1 (N3-C4-B5) angles (Table 3). Note that these different characteristics were comparable to the ones previously determined on BNNT and CNT by using the VASP code plus the van der Waals interaction (i.e., B-C equal to 1.63 Å, N-C equal to 1.54 Å and C-C equal to 1.58 Å) [11,12].
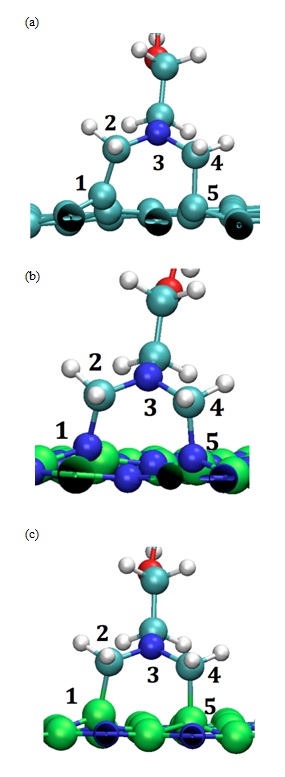
Figure 5: Optimized DFT Geometry of AzPt with (a) Defective GRN, (b) B defective BNN (i.e., BNN-1) (c) N-defective BNN (i.e., BNN-2). (B, N, C, O and H, atoms are represented as green, blue, cyan, red and white spheres respectively).

Figure 4: Optimized DFT geometry of (a) Defective GRN with H termination, (b) Lateral zoom in of (a), (c) Defective BNN with H termination (i.e., B defect noted BN-1), (d) Lateral zoom in of (c), (e) Defective BNN with H termination (i.e., N defect noted BN-2) (f) Lateral zoom in of (e). (B, N, C, and H, atoms are represented as green, blue, cyan and white spheres respectively).
Once the defective nanosheets were optimized, we have introduced the anticancer drug near the surface. For each case, the whole system was relaxed in order to minimize the total energy.
In the case of defective GRN two opposite carbon atoms of the same hexagon ring were concerned by the chemical reaction. It leads to a quasi-regular pentagon (Figure 5a). The adsorption energy was low since it reached -3.07 eV for the formation of two C–C bonds with the surface. The distance d1(C1-C2) and d2(C4-C5) were equal to 1.52 Å and 1.58 Å respectively and the angle measured between N3-C2-C1 atoms was equal to 116.71° while it reached 113.02° for the angle formed by N3-C4-C5 atom.
In the case of the BNN-1 a quasi-regular pentagon (Figure 5b) was also obtained with lower adsorption energy equal to -4.45 eV for the formation of two N-C bonds. The distances d1(N1-C2) and d2(C4-N5) were equal to 1.49 Å and 1.52 Å respectively. The angle N3-C2-N1 (N3-C4-N5) was equal to 114.43° (114.70°) as depicted in Figure 5-b. Results obtained in the case of BNN-2 were quite different despite the chemical creation of one pentamer (Figure 5-c). The adsorption energy equal to -2.56 eV for the formation of two B-C bonds was higher than for BNN-1. The distances of adsorption d1(B1-C2) and d2(C4-B5) were also slightly higher since they were equal to 1.65 Å and 1.70 Å, respectively. The analysis of the angle formation lead to values equal to 112.16° (109.11°) for N3-C2-B1 (N3-C4-B5) angles (Table 3). Note that these different characteristics were comparable to the ones previously determined on BNNT and CNT by using the VASP code plus the van der Waals interaction (i.e., B-C equal to 1.63 Å, N-C equal to 1.54 Å and C-C equal to 1.58 Å) [11,12].

Figure 5: Optimized DFT Geometry of AzPt with (a) Defective GRN, (b) B defective BNN (i.e., BNN-1) (c) N-defective BNN (i.e., BNN-2). (B, N, C, O and H, atoms are represented as green, blue, cyan, red and white spheres respectively).
| AzPt on GRN | AzPt on BNN-1 | AzPt on BNN-2 | |
| Distance/angle between C atoms of AzPt and atoms of the nanoflake surface | d1(C1-C2)=1.52 Å | d1(N1-C2)=1.49 Å | d1(B1-C2)=1.65 Å |
| d2(C4-C5)=1.58 Å | d2(C4-N5)=1.52 Å | d2(C4-B5)=1.70 Å | |
| N3-C2-C1=116.71° | N3-C2-N1=114.43° | N3-C2-B1=112.16° | |
| N3-C4-C5=113.02° | N3-C4-N5=114.70° | N3-C4-B5=109.11° | |
| Eadsorption (eV) | -3.07 eV | -4.45 eV | -2.56 eV |
Table 3: Distance angle and chemisorption energy of AzPt on defective nanoflake surfaces.
The short optimized distance determined after the AzPt adsorption on the defective structure could be a proof of a chemical bonding between the two interacting systems. To prove it we have calculated the charge Laplacian to determine the electronic density localization and thus the bonding nature between AzPt and the defective nanoflakes. In Figure 6, 3D representation of the AzPt-nanoflake Laplacians is reported with color scale varying from −0.4 to 0.4e / Å5. Negative value of ∇2 ρ(r)2 ρ(r) was always negative. This means that in these zones the potential energy is dominant and the negative charge are condensed. The electronic density was thus shared by both nuclei in all cases, i.e., concomitant with covalent or ionic interactions.
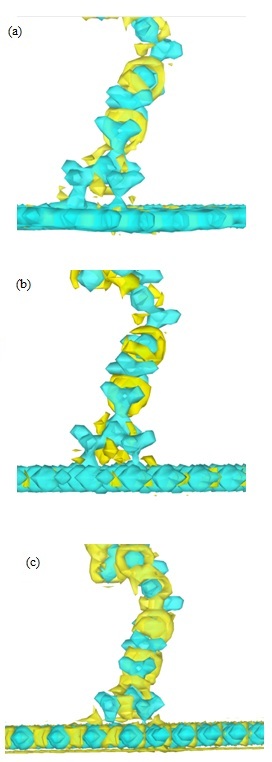
Figure 6: 3D representation of the charge density laplacian, AzPt-defective nanoflakes a) on defective GRN, (b) on B defective BNN-1, (c) on N defective BNN-2. Color scale varying of -0.4 at 0.4e / Å5. with blue for ∇2 ρ(r) < 0 and yellow for ∇2 ρ(r) > 0.
In parallel, we have studied the Bader charges of the different systems. For the AzPt adsorbed onto defective GRN we obtained a total Bader charge equal to 167.86 e. (167.75 e on BNN-1 surface and 167.70 e on BNN-2 surface (Table 4)). The total Bader charge fluctuations were not located on the whole molecule, since we observed only some small variations onto the Pt atom (only 0.01e) of AzPt and its nearest environment only.
The short optimized distance determined after the AzPt adsorption on the defective structure could be a proof of a chemical bonding between the two interacting systems. To prove it we have calculated the charge Laplacian to determine the electronic density localization and thus the bonding nature between AzPt and the defective nanoflakes. In Figure 6, 3D representation of the AzPt-nanoflake Laplacians is reported with color scale varying from −0.4 to 0.4e / Å5. Negative value of ∇2 ρ(r)2 ρ(r) was always negative. This means that in these zones the potential energy is dominant and the negative charge are condensed. The electronic density was thus shared by both nuclei in all cases, i.e., concomitant with covalent or ionic interactions.

Figure 6: 3D representation of the charge density laplacian, AzPt-defective nanoflakes a) on defective GRN, (b) on B defective BNN-1, (c) on N defective BNN-2. Color scale varying of -0.4 at 0.4e / Å5. with blue for ∇2 ρ(r) < 0 and yellow for ∇2 ρ(r) > 0.
In parallel, we have studied the Bader charges of the different systems. For the AzPt adsorbed onto defective GRN we obtained a total Bader charge equal to 167.86 e. (167.75 e on BNN-1 surface and 167.70 e on BNN-2 surface (Table 4)). The total Bader charge fluctuations were not located on the whole molecule, since we observed only some small variations onto the Pt atom (only 0.01e) of AzPt and its nearest environment only.
| AzPt alone | AzPt on defective GRN | AzPt on BN-1 | AzPt on BN-2 | |
| Pt | 9.30 | 9.27 | 9.27 | 9.27 |
| Cl | 7.237.25 | 7.227.25 | 7.237.24 | 7.237.24 |
| NH3 | 7.827.79 | 7.847.80 | 7.847.80 | 7.847.80 |
| Total charge | 39.39 | 39.38 | 39.38 | 39.38 |
Table 4: Covalent Bader’s charges (in elementary charge unit) located on Pt, Cl and N atoms of AzPt in different cases.
The comparison between results with AzPt agent deposited onto perfect or defective nanoflakes showed a charge loss up of 0.03 e on Pt atom. When the molecule was covalently attached on the defective nanoflakes we observed a slight diminution of the Pt cage charge equal to 0.01 e while it slightly. Increased (0.01 e) in the physisorption case (perfect nanoflakes). In overall cases, we can observe that the Pt valence charge was not modified and not implied in any electronic transfers. Such the electronic and the conformational stability of the therapeutic agent none covalently or covalently attached to the different nanoflakes were not affected. The role of the defect on a nanosheet was thus of a crucial importance. Indeed it allowed the chemical attachment of the AzPt without any impact on the drug molecule itself. Analyzing the energy interaction, it was very interesting to see that the adsorption of AzPt was always favored onto BNN compared to GRN. While many of experimental and theoretical works were dedicated to the properties of GRN, it seems very interesting from our results to develop other kinds of nanosheets in order to improve their properties. Note that experiments focused on the properties and the geometric characterizations of different nanoflakes were developed recently and in the article J.-B. Wu et al., [32]. This would open further studies for novel applications using these 2D nanosurfaces.
The comparison between results with AzPt agent deposited onto perfect or defective nanoflakes showed a charge loss up of 0.03 e on Pt atom. When the molecule was covalently attached on the defective nanoflakes we observed a slight diminution of the Pt cage charge equal to 0.01 e while it slightly. Increased (0.01 e) in the physisorption case (perfect nanoflakes). In overall cases, we can observe that the Pt valence charge was not modified and not implied in any electronic transfers. Such the electronic and the conformational stability of the therapeutic agent none covalently or covalently attached to the different nanoflakes were not affected. The role of the defect on a nanosheet was thus of a crucial importance. Indeed it allowed the chemical attachment of the AzPt without any impact on the drug molecule itself. Analyzing the energy interaction, it was very interesting to see that the adsorption of AzPt was always favored onto BNN compared to GRN. While many of experimental and theoretical works were dedicated to the properties of GRN, it seems very interesting from our results to develop other kinds of nanosheets in order to improve their properties. Note that experiments focused on the properties and the geometric characterizations of different nanoflakes were developed recently and in the article J.-B. Wu et al., [32]. This would open further studies for novel applications using these 2D nanosurfaces.
CONCLUSION
We have investigated by performing DFT calculations, interactions between amino derivative Pt anticancer drug and graphene BN non defective and defective nanoflakes. Geometrics and energetics optimization of the different systems were done by considering different possible atomic interacting configurations of the anticancer molecule on the nanoflakes. Simulation results have showed that only physisorption could occur between the molecule and the perfect nanoflakes (i.e., without vacancy). The interaction between the molecule and the defective nanoflake surfaces were more complex. Adsorption on B defective BNN-1 surface showed a strong chemisorption due to the boron defect. On the contrary, the chemisorption on N defective BNN-2 nanoflake was the less stable while the adsorption energy on defective GRN was intermediate. Moreover, all theoretical results have showed that the anticancer agent was very slightly affected when it was in interaction with the nanoflake structures. These results provide an interesting basis on the role of graphene and BN nanoflakes as an inert nanocarrier of active platinum drug molecule toward side cells. In order to stick with the medicine experimental therapy, we want to pursuit our theoretical simulation with the graphene or BN oxide nanoflakes which represent some strong potential applications.
ACKNOWLEDGEMENT
Calculations were performed with the supercomputer regional facility Mesocenter of the University of Franche-Comté.
REFERENCES
- Jamieson T, Bakhshi R, Petrova D, Pocock R, Imani M, et al. (2007) Biological applications of quantum dots. Biomaterials 28: 4717-4732.
- Wagstaff AJ, Brown SD, Holden MR, Craig GE, Plumb JA, et al. (2012) Cisplatin drug delivery using gold-coated iron oxide nanoparticles for enhanced tumour targeting with external magnetic fields. Inorganica Chimica Acta 393: 328-333.
- Craig GE, Brown SD, Lamprou DA, Graham D, Wheate NJ (2012) Cisplatin-tethered gold nanoparticles that exhibit enhanced reproducibility, drug loading, and stability: a step closer to pharmaceutical approval? Inorg Chem 51: 3490-3507.
- Tan A, De La Peña H, Seifalian AM (2010) The application of exosomes as a nanoscale cancer vaccine. Int J Nanomedicine 5: 889-900.
- Murakami M, Cabral H, Matsumoto Y, Wu S, Kano MR, et al. (2011) Improving drug potency and efficacy by nanocarrier-mediated subcellular targeting. Sci Transl Med 3: 64.
- Chang TM, Prakash S (2001) Procedures for microencapsulation of enzymes, cells and genetically engineered microorganisms. Mol Biotechnol 17: 249-260.
- Bawa R (2009) NanoBiotech 2008: Exploring global advances in nanomedicine. Nanomedicine 5: 5-7.
- Khemir H, Tangour B, Moussa F (2015) In Silico Study of Spacer Arm Length Influence on Drug Vectorization by Fullerene C60. Journal of Nanomaterials 2015: 374218.
- Khemir H, Tangour B, Moussa F (2016) An “In Silico” Study of Drug Vectorization by a Carbon Nanocone. Journal of Computational and Theoretical Nanoscience 13: 3384-3392.
- Hosni Z, Bessrour R, Tangour B (2014) 195Pt Chemical Shift Ability to Control the Antitumor Drug Cisplatin Encapsulated Into Carbon Nanotubes: A Theoretical Study. Journal of Computational and Theoretical Nanoscience 11: 318-323.
- Kraszewski S, Duverger E, Ramseyer C, Picaud F (2013) Theoretical study of amino derivatives and anticancer platinum drug grafted on various carbon nanostructures. J Chem Phys 139: 174704.
- Duverger E, Gharbi T, Delabrousse E, Picaud F (2014) Quantum study of boron nitride nanotubes functionalized with anticancer molecules. Phys Chem Chem Phys 16: 18425-18432.
- Ciesielski A, Samorì P (2014) Graphene via sonication assisted liquid-phase exfoliation. Chem Soc Rev 43: 381-398.
- Hohenberg P, Kohn W (1964) Inhomogeneous Electron Gas. Phys Rev 136: 864.
- Kohn W, Sham LJ (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review 140: 1133-1138.
- Perdew JP, Burke K, Ernzerhof M (1996) Generalized Gradient Approximation Made Simple. Phys Rev Lett 77: 3865-3868.
- Ordejon P, Artacho E, Soler JM (1996) Self-consistent order-N density-functional calculations for very large systems. Phys Rev B 53: 10441-10444.
- Schwarz K, Blaha P (2003) Solid state calculations using WIEN2k. Computational Materials Science 28: 259-273.
- Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, et al. (2009) Gaussian 09, Revision B.01. Expanding the limits of computational Chemistry. Gaussian Inc, Wallingford CT, USA.
- Paier J, Marsman M, Hummer K, Kresse G, Gerber IC, et al. (2006) Screened hybrid density functionals applied to solids. J Chem Phys 124: 154709.
- Kiejna A, Kressse G, Rogal J, De Sarkar A, Reuter K, et al. (2006) Comparison of the full-potential and frozen-core approximation approaches to density-functional calculations of surfaces. Phys Rev B 73: 035404.
- Henkelman G, Arnaldsson A, Jonsson H (2006) A fast and robust algorithm for Bader decomposition of charge density. Computational Materials Science 36: 354-360.
- Tang W, Sanville E, Henkelman G (2009) A grid-based Bader analysis algorithm without lattice bias. J Phys Condens Matter 21: 084204.
- Bader RFW, Jones GA (1961) The Hellmann-Feynman Theorem and Chemical Binding. Canadian Journal of Chemistry 39: 1253-1265.
- Matta CF, Boyd R (2007) Wiley, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, Wiley Online Library, New Jersey, USA.
- Bader RFW (1991) A quantum theory of molecular structure and its applications. Chem Rev 91: 893-928.
- Bader RFW (1988) From Schrödinger to atoms in molecules. Pure Appl Chem 60: 145-155.
- Kundalwal SI, Meguid SA, Weng GJ (2017) Strain gradient polarization in graphene. Carbon 117: 462-472.
- Maggini M, Scorrano G, Prato M (1993) Addition of azomethine ylides to C60: synthesis, characterization, and functionalization of fullerene pyrrolidines. J Am Chem Soc 115: 9798-9799.
- Singh P, Campidelli S, Giordani S, Bonifazi D, Bianco A, et al. (2009) Organic functionalisation and characterisation of single-walled carbon nanotubes. Chem Soc Rev 38: 2214-2230.
- Quintana M, Spyrou K, Grzelczak M, Browne WR, Rudolf P, et al. (2010) Functionalization of graphene via 1,3-dipolar cycloaddition. ACS Nano 4: 3527-3533.
- Wu JB, Zhang X, Ijäs M, Han WP, Qiao XF, et al. (2014) Resonant Raman spectroscopy of twisted multilayer graphene. Nat Commun 5: 5309.
Citation: Duverger E, Bentin J, Delabrousse E, Gharbi T, Picaud F (2017) Ab Initio Study of Azomethine Derivative Cancer Drug on Boron Nitride and Graphene Nanoflakes. J Nanotechnol Nanomed Nanobiotechnol 4: 014.
Copyright: © 2017 Fabien Picaud, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Journal Highlights
© 2026, Copyrights Herald Scholarly Open Access. All Rights Reserved!
