
Advances in Microbiology Research Category: Microbiology
Type: Review Article
Analysis of Antibody by Real-Valued Special Functions
*Corresponding Author(s):
Bin ZhaoCollege Of Science, Northwest A&F University, Yangling, Shaanxi, China
Tel:+86 13028517572,
Email:zhaobin835@nwsuaf.edu.cn
Received Date: Sep 20, 2017
Accepted Date: Jan 11, 2018
Published Date: Jan 26, 2018
Abstract
Along with the rapid development of genetic engineering technology and antibody engineering technology, humanized monoclonal antibody has been rapidly developed and gradually replaces the rat sourced monoclonal antibody. In this paper, we establish two new logarithmically completely monotonic functions involving the gamma function according to two preferred interaction geometries, necessary and sufficient conditions are presented for one of them to be logarithmically completely monotonic. As a consequence, a sharp inequality involving the gamma function is deduced to solve the problems of genetically engineered antibody.
Keywords
Gamma function; Genetically engineered antibody; Logarithmically completely monotonic; inequality; PSI function
INTRODUCTION
Antibodies have been proven to be indispensable tools for biomedical applications. Different engineered antibodies have been developed for various purposes according to the amino acid sequence and/or spatial structure of protein (Figure 1). At present, it is still difficult to predict the optimal structure of antibodies. Topology knowledge can be important in antibody application as well as transformation. Theoretically, we can obtain desired antibodies by using protein/gene engineering technology. For instance, we can transform the Complementarity Determining Region (CDR) to promote the affinity of the antibody to antigen. Similarly, we could also transform any domain of antibody to make it bind with any desired target. Under this vision, topology is a powerful tool to predict the structure of protein and it will serve to antibody engineering. Our present work tries to explain, and predict, if possible, the change of structure, size and function of antibodies as well as their fragments from a topological perspective.
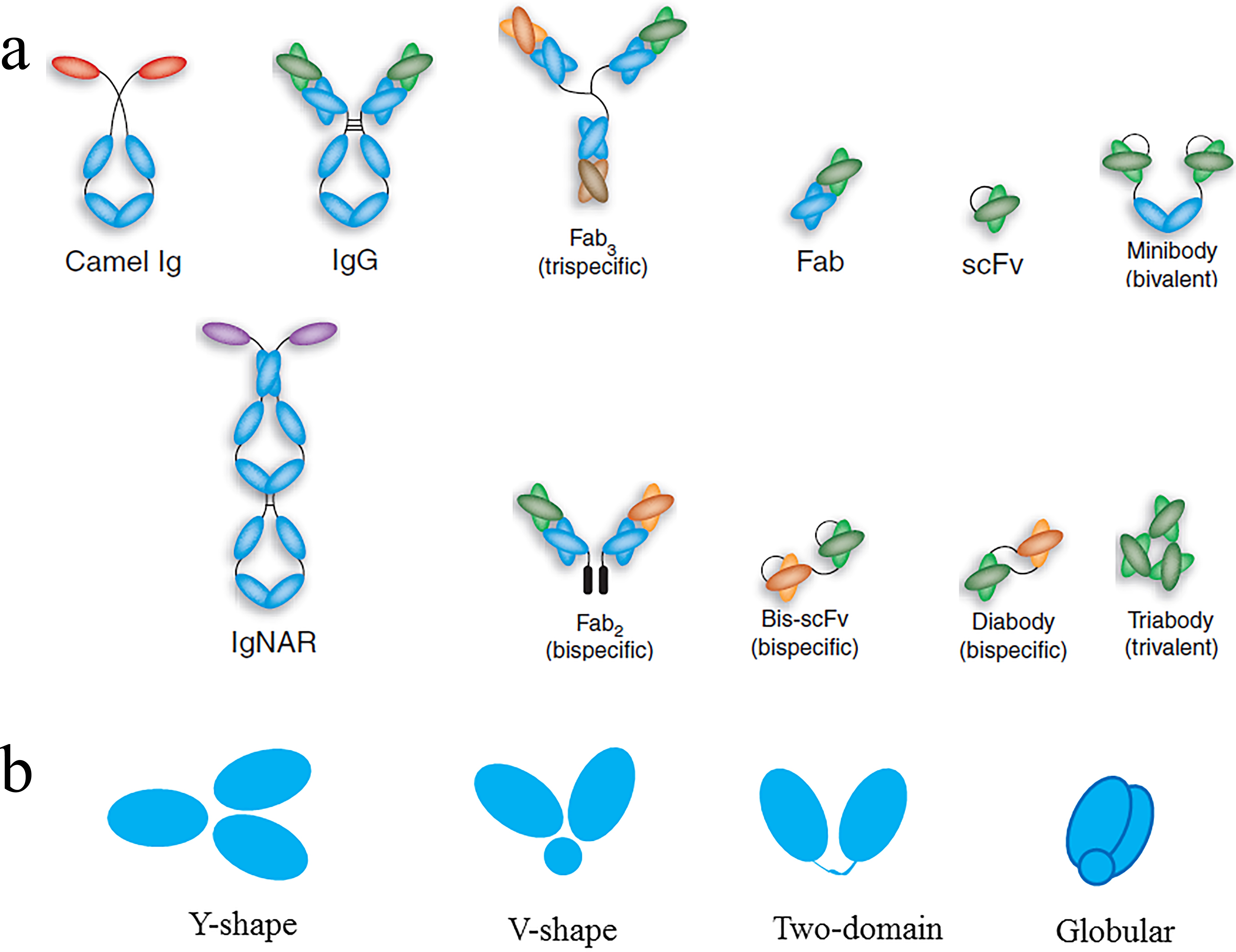
Figure 1: Different antibody formats. (a) Different antibody or engineered antibodies. (b) Different shape of antibody.
For the classical Euler’s gamma function and psi (digamma) function are defined by respectively.
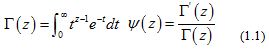
The derivatives for are known as polygamma functions. For (see [1]), the following series representations are established:
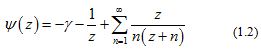
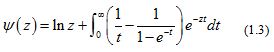
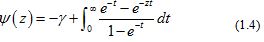
where denotes the Euler’s constant.
We next recall [2-5] that a function is said to be completely monotonic on an interval , if has derivatives of all orders on which alternate successively in sign, that is,
for all and for all . If inequality (1.5) is strict for all and all , then is said to be strictly completely monotonic.
The classical Bernstein–Widder theorem [6, p. 160, Theorem 12a] states that a function is completely monotonic on if and only if it is a Laplace transform of some nonnegative measure , that is,
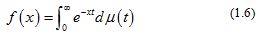
where is non-decreasing and the integral converges for .
We recall also [7-9] that a positive function is said to be logarithmically completely monotonic on an interval if has derivatives of all orders on and
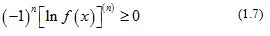
for all and for all . If inequality (1.7) is strict for all and all , then is said to be strictly logarithmically completely monotonic.
The antibody structure will be changed when it binds certain targets (Figure 2a), i.e., antigen, receptor. How to describe the changes in the view of topology? The following cases will explain it in detail.
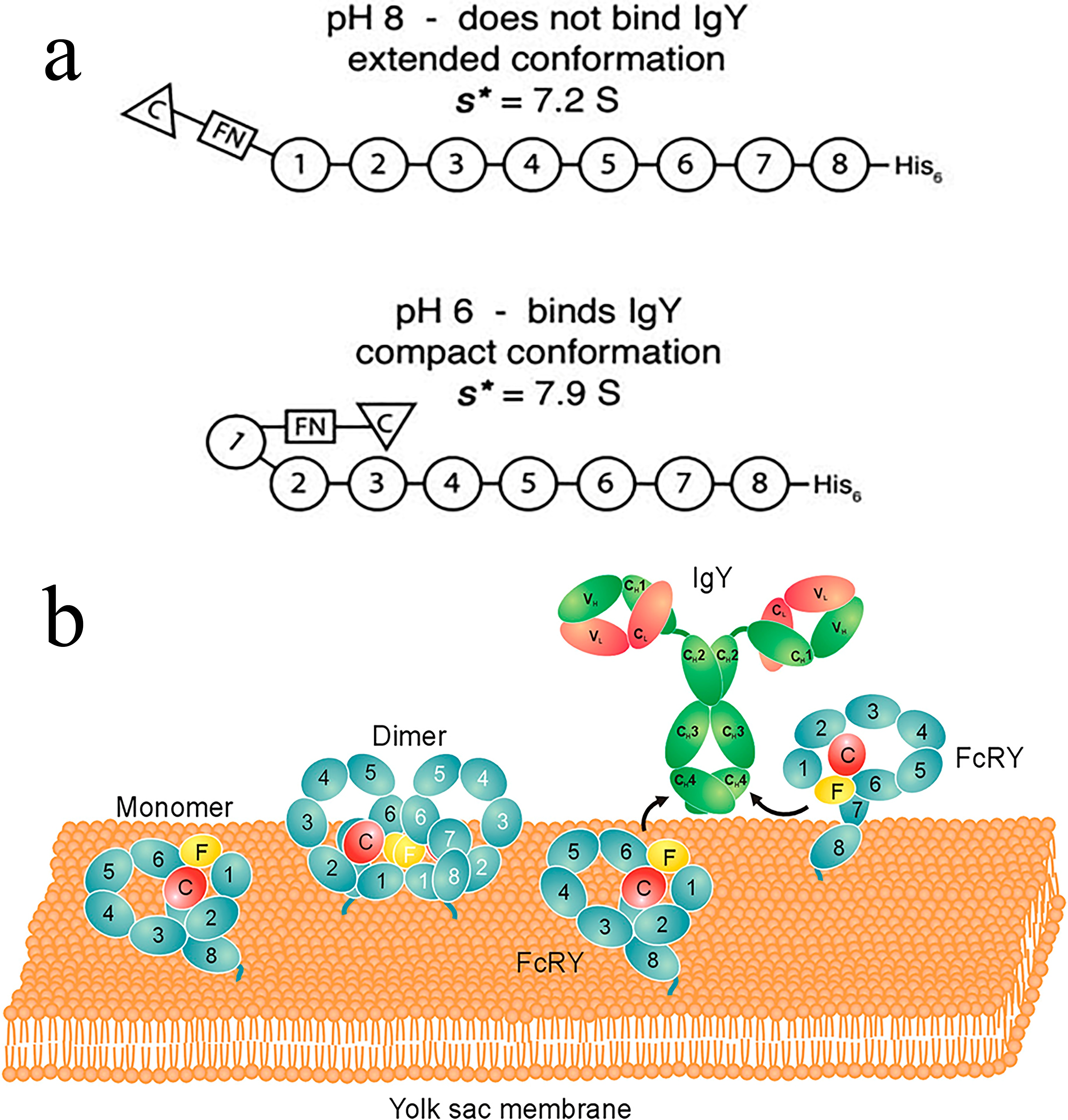
Figure 2: Model of pH-dependent conformational change of FcRY and structures for the FcRY monomer and dimer. (a) FcRY has an extended conformation at pH 8 (s*= 7.2 S) with no predicted interaction between the CysR-FNII domains and the CTLDs. At pH 6 the CysR-FNII region folds back and binds to the CTLDs, resulting in a more compact conformation (s*= 7.9 S) that is able to bind IgY.
(b) Likely orientations of FcRY and FcRY-IgY on a membrane. The two FcRY monomers on the Right are shown in an orientation that would allow formation of a 2:1 FcRY-IgY complex.
(b) Likely orientations of FcRY and FcRY-IgY on a membrane. The two FcRY monomers on the Right are shown in an orientation that would allow formation of a 2:1 FcRY-IgY complex.
It was proved explicitly in [8] and other articles that a logarithmically completely monotonic function must be completely monotonic.
In [10], G. D. Anderson et al. proved that the function
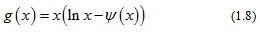
is strictly decreasing and strictly convex on , with two limits
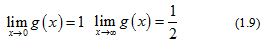
From (1.9) and the monotonicity of , then the double inequalities
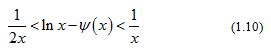
holds for all .
In [11, Theorem 1], by using the well-known Binet's formula, H. Alzer generalized the monotonicity and convexity of , that is, the function is strictly completely monotonic on if and only if .
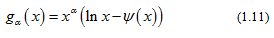
In [12], D. Kershaw and A. Laforgia proved that the function is decreasing on and is increasing on . These are equivalent to the function being increasing and being decreasing on , respectively.
In [13, Theorem 5], F. Qi and Ch.-p. Chen generalized these functions. They obtained the fact that for all the function is strictly increasing for and strictly decreasing for , respectively.
After the papain digestion, the remained antibody functional part (usually the Fab domain), will be smaller and the structure is also changed (Figure 1b). These changes can be revealed vividly using topology. Recently [14, Theorem 1], F. Qi, C.-F Wei and B.-N Guo established another excellent result, which states that forgiven and , let
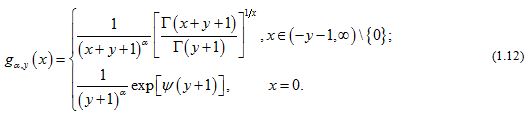
The function (1.12) is logarithmically completely monotonic with respect to if and only if ; and if , the reciprocal of the function (1.12) is logarithmically completely monotonic with respect to .
Antibodies occur spontaneously gathering and forming dimer, polymer, which will influence their functions (Figure 2b). In antibody engineering practice, it urgently needs some measures to overcome this difficulty. From topology perspective, we could understand this issue as follow.
Stimulated by the above results, we put forward the function as follows: forgiven and real number , let the function be defined by our first result is contained in the following theorem.
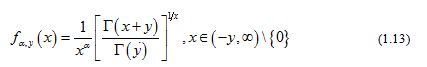
Theorem 1
For the function (1.13), then the following statements are true:
(1) for any given , the function (1.13) is strictly logarithmically completely monotonic with respect to if and only if ;
(2) for any given , if , then the function (1.13) is strictly logarithmically completely monotonic with respect to ;
(3) for any given , the reciprocal of the function (1.13) is strictly logarithmically completely monotonic with respect to if and only if .our second result is presented in the following theorem.
(1) for any given , the function (1.13) is strictly logarithmically completely monotonic with respect to if and only if ;
(2) for any given , if , then the function (1.13) is strictly logarithmically completely monotonic with respect to ;
(3) for any given , the reciprocal of the function (1.13) is strictly logarithmically completely monotonic with respect to if and only if .our second result is presented in the following theorem.
Theorem 2
For any given , let the function be defined on by
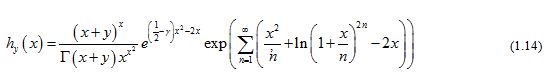
where denotes the Euler’s constant, then the function (1.14) is strictly logarithmically completely monotonic with respect to on .
The following corollary can be derived from Theorems 2 immediately.
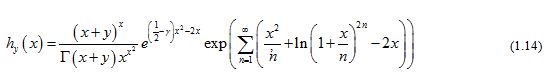
where denotes the Euler’s constant, then the function (1.14) is strictly logarithmically completely monotonic with respect to on .
The following corollary can be derived from Theorems 2 immediately.
Corollary 1
For any given , the inequality holds for all .
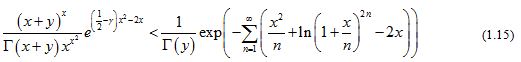
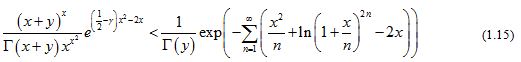
Lemma
In order to prove our main results, we need the following lemmas.
It is well known that Bernoulli polynomials and Euler polynomials are defined by respectively [15].
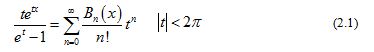
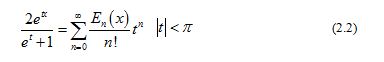
The Bernoulli numbers are denoted by , while the Euler numbers are defined by .
In [16], the following summation formula is given:
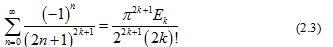
for any nonnegative integer , which implies
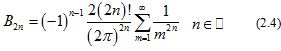
In particular, it is known that for all we have
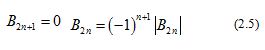
And the first few nonzero values are (see [17, p.804, Chapter23]).
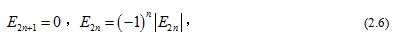
The Bernoulli and Euler numbers and polynomials are generalized [18-21].
It is well known that Bernoulli polynomials and Euler polynomials are defined by respectively [15].
The Bernoulli numbers are denoted by , while the Euler numbers are defined by .
In [16], the following summation formula is given:
for any nonnegative integer , which implies
In particular, it is known that for all we have
And the first few nonzero values are (see [17, p.804, Chapter23]).
The Bernoulli and Euler numbers and polynomials are generalized [18-21].
Lemma 1 [22,23]
For real number and natural number , then
Remark 1
, , , only depend on natural number .
Lemma 2 [24, Lemma 3]
For real number and natural number , we have
Lemma 3 [1,17]
For real number and natural number , we have
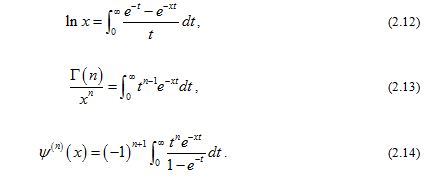
Lemma 4
Let the sequence of functions for be defined on by
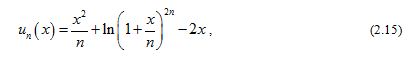
the series is differentiable on , that is,
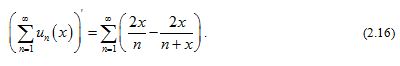
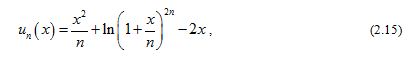
the series is differentiable on , that is,
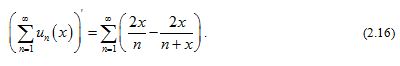
Proof
It is obvious that , therefore converges at . In order to prove (2.16), we need only to show that the inner closed uniform convergence of the series on . From (2.15), we have
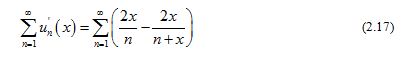
For any interval , we have
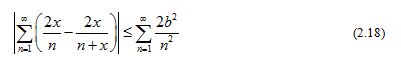
for all . It is easy to check that the series converges, which and Weierstrass M-test implies that the series is inner closed uniformly convergent on . Hence the series is differentiable on and the identity (2.17) holds for .
The lemma is proved.
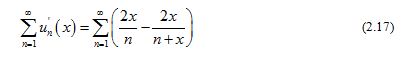
For any interval , we have
for all . It is easy to check that the series converges, which and Weierstrass M-test implies that the series is inner closed uniformly convergent on . Hence the series is differentiable on and the identity (2.17) holds for .
The lemma is proved.
Lemma 5
For and real number , let the function be defined by
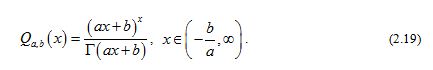

If , then the function (2.19) satisfies
for all and .
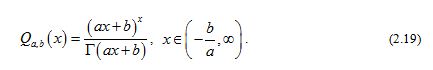

If , then the function (2.19) satisfies
for all and .
Proof
Taking the logarithm of yields

and differentiating , then
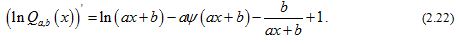
For given integer , we get
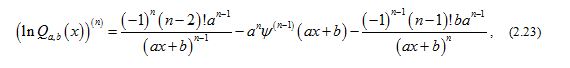
and, by the identities (2.13) and (2.14), (2.23) can be written as
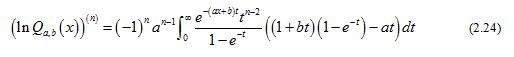
Let and . It is easy to check that
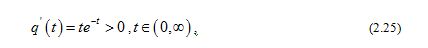
therefore is strictly increasing on , and then .
The following two cases will complete the proof of Lemma 5.
and differentiating , then
For given integer , we get
and, by the identities (2.13) and (2.14), (2.23) can be written as
Let and . It is easy to check that
therefore is strictly increasing on , and then .
The following two cases will complete the proof of Lemma 5.
Case 1
If , then since for , we have
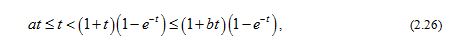
which implies , and then for all .
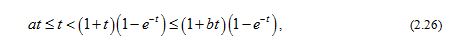
which implies , and then for all .
Case 2
If , then we get
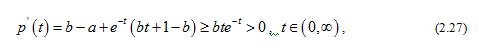
, , (2.27)
therefore is strictly increasing on , and then .
From (2.24), we know that the inequality (2.20) holds for and integer .
The lemma is proved. •
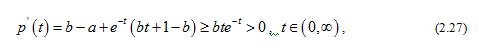
, , (2.27)
therefore is strictly increasing on , and then .
From (2.24), we know that the inequality (2.20) holds for and integer .
The lemma is proved. •
Proof of Theorems
Proof of Theorem 1
For and natural number , taking the logarithmically differential into consideration yields
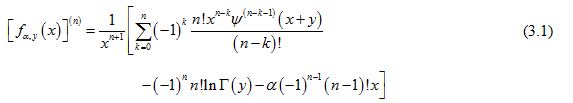
where and stand for and respectively.
Furthermore, differentiating directly gives
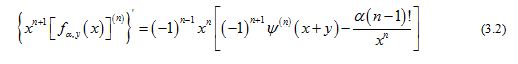
Making use of (2.11) and (2.13) shows that for all and any fixed , the double inequality
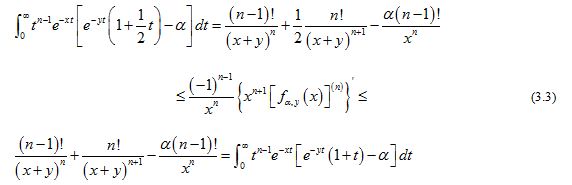
holds for all and .
For any fixed , let and be defined on by respectively.
Differentiating and directly, we obtain
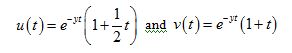
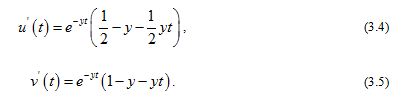
Therefore, for given we have

and

From (3.6) and (3.7), we conclude that for all we obtain

and
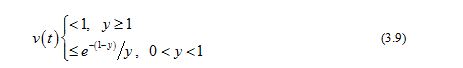
From (3.3) and (3.8)-(3.9), it is easy to see that
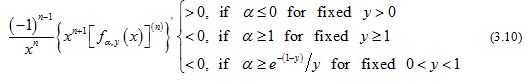
for all and all .
On the one hand, if , then the inequalities (3.10) can be equivalently changed into
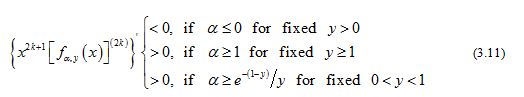
and
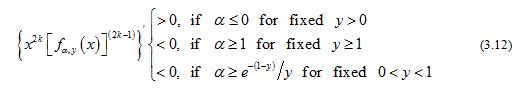
for .
From (3.1), then simple computation shows that

for all and any given . As a result,
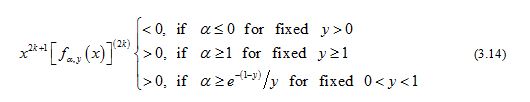
and

for all and all .
Therefore, (3.14) and (3.15) imply
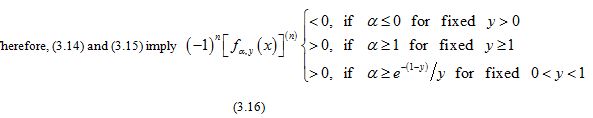
for all and all .
Hence, if either for given or for given , the function (1.13) is strictly logarithmically completely monotonic with respect to on , and if for given , so is the reciprocal of the function (1.13).
On the other hand, if for any given , then (3.10) implies
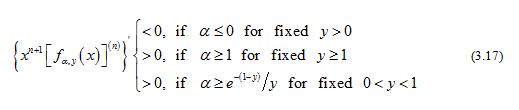
for .
In view of (3.13), we can conclude that
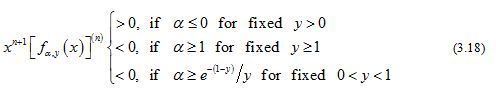
for . It is obvious that (3.18) is equivalent to that (3.14) and (3.15) hold for any given and . Therefore, it is easy to prove similarly that (3.16) is also valid on for any given and all .
The amino acid of antibody/protein possesses different preferences. Thus we can conduct site-directed mutation to promote the affinity and/or hydrophilic with the prediction of topology. For example, bovine antibodies have an unusual structure comprising a β-strand ‘stalk’ domain and a disulphide-bonded ‘knob’ domain in CDR3 (Figure 3). Attempts have been made to utilize such amino acid preference for antibody drug development.
where and stand for and respectively.
Furthermore, differentiating directly gives
Making use of (2.11) and (2.13) shows that for all and any fixed , the double inequality
holds for all and .
For any fixed , let and be defined on by respectively.
Differentiating and directly, we obtain
Therefore, for given we have
and
From (3.6) and (3.7), we conclude that for all we obtain
and
From (3.3) and (3.8)-(3.9), it is easy to see that
for all and all .
On the one hand, if , then the inequalities (3.10) can be equivalently changed into
and
for .
From (3.1), then simple computation shows that
for all and any given . As a result,
and
for all and all .
Therefore, (3.14) and (3.15) imply
for all and all .
Hence, if either for given or for given , the function (1.13) is strictly logarithmically completely monotonic with respect to on , and if for given , so is the reciprocal of the function (1.13).
On the other hand, if for any given , then (3.10) implies
for .
In view of (3.13), we can conclude that
for . It is obvious that (3.18) is equivalent to that (3.14) and (3.15) hold for any given and . Therefore, it is easy to prove similarly that (3.16) is also valid on for any given and all .
The amino acid of antibody/protein possesses different preferences. Thus we can conduct site-directed mutation to promote the affinity and/or hydrophilic with the prediction of topology. For example, bovine antibodies have an unusual structure comprising a β-strand ‘stalk’ domain and a disulphide-bonded ‘knob’ domain in CDR3 (Figure 3). Attempts have been made to utilize such amino acid preference for antibody drug development.
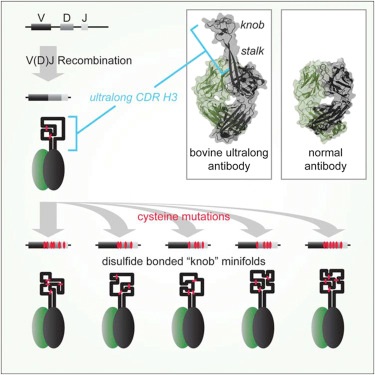
Figure 3: Unique Structural Domain in Bovine IgG antibodies and application.
Consequently, the function (1.13) is the same logarithmically completely monotonicity on as on , that is, if either for given or for given , the function (1.13) is strictly logarithmically completely monotonic with respect to on , and if forgiven , so is the reciprocal of the function (1.13).
Conversely, we assume that the reciprocal of the function (1.13) is strictly logarithmically completely monotonic on for any given . Then we have for any given and all
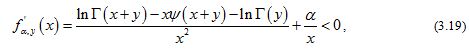
which implies
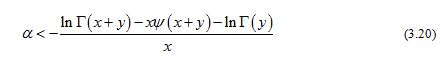
By L’Hˆospital’s rule, we have
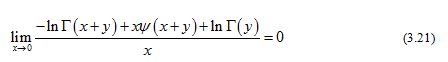
for any given . By virtue of (3.20) and (3.21), we conclude that the necessary condition for the reciprocal of the function (1.13) to be strictly logarithmically completely monotonic is .
If the function (1.13) is logarithmically completely monotonic on
for any given , then the inequality (3.19) and (3.20) are reversed for any given and all .
By utilizing (2.7) and (2.8), it is easy to see that
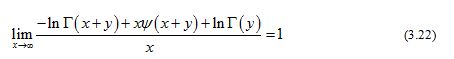
for any given . In fact, it is not difficult to show that the necessary condition for the function (1.13) to be strictly logarithmically completely monotonic is .
The proof of Theorem 1 is completed. •
Consequently, the function (1.13) is the same logarithmically completely monotonicity on as on , that is, if either for given or for given , the function (1.13) is strictly logarithmically completely monotonic with respect to on , and if forgiven , so is the reciprocal of the function (1.13).
Conversely, we assume that the reciprocal of the function (1.13) is strictly logarithmically completely monotonic on for any given . Then we have for any given and all
which implies
By L’Hˆospital’s rule, we have
for any given . By virtue of (3.20) and (3.21), we conclude that the necessary condition for the reciprocal of the function (1.13) to be strictly logarithmically completely monotonic is .
If the function (1.13) is logarithmically completely monotonic on
for any given , then the inequality (3.19) and (3.20) are reversed for any given and all .
By utilizing (2.7) and (2.8), it is easy to see that
for any given . In fact, it is not difficult to show that the necessary condition for the function (1.13) to be strictly logarithmically completely monotonic is .
The proof of Theorem 1 is completed. •
Proof of Theorem 2
Taking the logarithm of gives
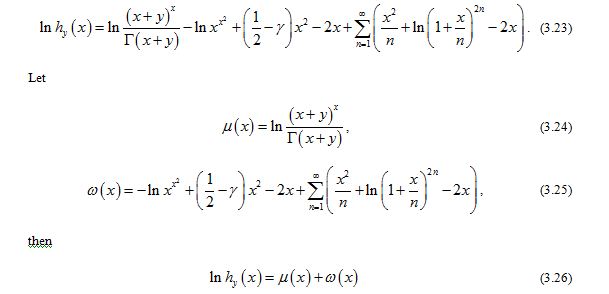
Let
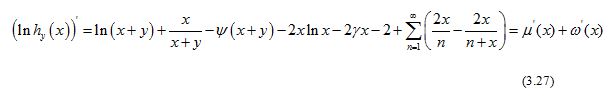
then
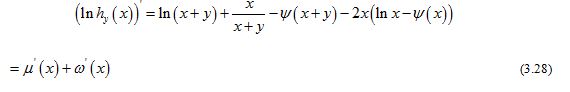
In view of Lemma 4, straightforward calculation gives

By virtue of (1.2), the identity (3.27) is equivalent to

By Lemma 5, we know that is strictly increasing on , which and (1.10) imply the limit of equals 1 as , therefore holds for all .
We know that is strictly completely monotonic on , where is defined by (1.8), hence for given integer , the inequality holds for all .

And then by using inequality (1.9) and (1.10), we get for all .
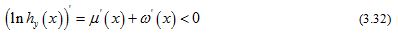
From (3.29) and (3.31), we conclude that
for all . Utilizing Lemma 5 and (3.30), for given integer , it is easy to see that
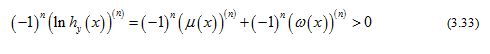
for all .
Theorem 2 follows from (3.32) and (3.33).
Thus the proof of Theorem 2 is completed.
Let
then
In view of Lemma 4, straightforward calculation gives
By virtue of (1.2), the identity (3.27) is equivalent to
By Lemma 5, we know that is strictly increasing on , which and (1.10) imply the limit of equals 1 as , therefore holds for all .
We know that is strictly completely monotonic on , where is defined by (1.8), hence for given integer , the inequality holds for all .
And then by using inequality (1.9) and (1.10), we get for all .
From (3.29) and (3.31), we conclude that
for all . Utilizing Lemma 5 and (3.30), for given integer , it is easy to see that
for all .
Theorem 2 follows from (3.32) and (3.33).
Thus the proof of Theorem 2 is completed.
REFERENCES
- Erdélyi A, Magnus W, Oberhettinger F, Tricomi FG (1955) Higher transcendental functions-Vol I, II, III. McGraw-Hill, New York, USA.
- Bernstein S (1929) Sur les fonctions absolument monotones. Acta Math 52: 1-66.
- Hausdorff F (1921) Summationsmethoden und Momentfolgen I. Mathematische Zeitschrift 9: 74-109.
- Qi F, Chen CP (2004) A complete monotonicity property of the gamma function. Journal of Mathematical Analysis and Applications 2: 603-607.
- Widder DV (1931) Necessary and sufficient conditions for the representation of a function as a La- place integral. Trans Amer Math Soc 33: 851-892.
- Widder DV (1941) The Laplace Transform. Princeton University Press, Princeton, New Jersey, USA.
- Atanassov RD, Tsoukrovski UV (1988) Some properties of a class of logarithmically completely monotonic functions. C R Acad Bulgare Sci 41: 21-23.
- Berg C (2004) Integral representation of some functions related to the gamma function. Mediterranean Journal of Mathematics 1: 433-439.
- Grinshpan AZ, Ismail MEH (2006) Completely monotonic functions involving the gamma and q-gamma functions. American Mathematical Society 134: 1153-1160.
- Anderson GD, Barnard RW, Richards KC, Vamanamurthy MK, Vuorinen M (1995) Inequalties for zero-balanced hypergeometric functions. American Mathematical Society 347: 1713-1723.
- Alzer H (1997) On some inequalities for the gamma and psi functions. Mathematics of Computation 66: 373-389.
- Kershaw D, Laforgia A (1985) Monotonicity results for the gamma function. Journal of Inequalities in Pure and Applied Mathematics 119: 127-133.
- Qi F, Chen CP (2004) Monotonicity and convexity results for functions involving the gamma function. J Appl Math Sci 1: 27-36.
- Qi F, Wei CF, Guo BN (2012) Complete monotonicity of a function involving the ratio of gam- ma functions and applications. Banach Journal of Mathematical Analysis 6: 35-44.
- Guo BN, Qi F (2010) A property of logarithmically absolutely monotonic functions and the loga- rithmically complete monotonicity of a power-exponential function, Politehn. Appl Math Phys 72: 21-30.
- Wang ZX, Guo DR (2000) Introduction to Special Function: The Series of Advanced Physics of Peking University. Peking University Press, Beijing, China.
- Abramowitz M, Stegun IA (1964) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Courier Corporation, Massachusetts,USA.
- Guo BN, Qi F (2002) Generalization of Bernoulli polynomials. International Journal of Mathematical Education in Science and Technology 33: 428-431.
- Luo QM, Guo BN, Qi F, Debnath L (2003) Generalizations of Bernoulli numbers and polynomials. International Journal of Mathematics and Mathematical Sciences 2003: 3769-3776.
- Luo QM, Qi F (2003) Relationships between generalized Bernoulli numbers and polynomials and generalized Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 7: 11-18.
- Luo QM, Qi F, Debnath L (2003) Generalizations of Euler numbers and polynomials. International Journal of Mathematics and Mathematical Sciences 2003: 3893-3901.
- Qi F, Guo BN (2005) Monotonicity and convexity of ratio between gamma functions to different powers. Journal of the Indonesian Mathematical Society 11: 39-49.
- Fichtenholz GM (1964) Differential- und Integralrechnung. Vol II. VEB Deutscher Verlagder Wissenschaften, Berlin, Germany.
- Guo BN, Qi F (2010) Two new proofs of the complete monotonicity of a function involving the psi function. Bull Korean Math Soc 47: 103-111.
- Andrew M Scott, Jedd D Wolchok, Lloyd J (2012) Antibody therapy of cancer. Nature reviews 12: 278-287.
- Carlos F, Lucia R, Jeffrey W (1993) High-affinity self-reactive human antibodies by design andselection: Targeting the integrin ligand binding site. Proc Natl Acad Sci U S A 90: 10003-10007.
- Miroslava O, Xavier E (2005) Human genetics moves from clinic to bench - and back. Genome Biology 6: 343.
- Repp R, Hvan Ojik H, Valerius T, Groenewegen G, Wieland G, et al. (2003) Phase I clinical trial of the bispecific antibody MDX-H210 (anti-FcgRI anti-HER-2/neu) in combination with Filgrastim (G-CSF) for treatment of advanced breast cancer. Br J Cancer 89: 2234-2243.
- Alinari L, Lapalombella R, Andritsos L, Baiocchi RA, Lin TS, et al. (2007) Alemtuzumab (Campath-1H) in the treatment of chronic lymphocytic leukemia. Oncogene 26: 3644-3553.
- Jane C, Wilbert H, Hauger SB, Janai H, Bastian JF, et al. (2005) Infliximab treatment for refractory Kawasaki syndrome. J Pediatr 146: 662-667.
Citation: Zhao B, Cao J, Liang L, Li A (2018) Analysis of Antibody by Real-Valued Special Functions. Adv Microb Res 2: 003.
Copyright: © 2018 Bin Zhao, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Journal Highlights
© 2026, Copyrights Herald Scholarly Open Access. All Rights Reserved!
