
Maxwell Equations and Light Propagation in Rotating Frames
*Corresponding Author(s):
Sfarti ADepartment Of Computer Science, University Of California, 387 Soda Hall, Berkeley, United States
Email:egas@pacbell.net
Abstract
In the current paper we present a generalization of the Maxwell equations in a frame in uniform circular motion with respect to an inertial frame of reference. We show an immediate application to the propagation of electromagnetic waves in frames in uniform rotation. The solution is of great interest for real time applications because earth-bound laboratories are inertial only in approximation. The motivation is that the real life applications include accelerating and rotating frames with arbitrary orientations more often than the idealized case of inertial frames; our daily experiments happen in the laboratories attached to the rotating Earth. We are interested in deriving the Maxwell equations in rotating frames of reference. Our paper deals with centrally rotating frame.
Keywords
General coordinate transformations; Light propagation in uniformly rotating frames; Maxwell equations and Uniform rotation motion
PACS
03.30, +p, 52.20.Dq, 52.70.Nc
Introduction
Real life applications include accelerating and rotating frames more often than the idealized case of inertial frames. Our daily experiments happen in the laboratories attached to the rotating, continuously accelerating Earth. Usually, such experiments are explained from the perspective of an external, inertial frame because special relativity in rotating frames is viewed as more complicated. In the present paper, we will construct a straightforward explanation by applying the formalisms developed in previous work [1-7].
The euler-lagrange equations for motion on a uniformly rotating disc
In an inertial frame K the coordinates are (Τ, R, Φ, Z). In a frame K ' rotating with respect the inertial frame, the coordinates are (t,r,ø, z) . The angular speed of rotation between the two frames is Ω. The transformation between the frames is [8] (Figure 1):
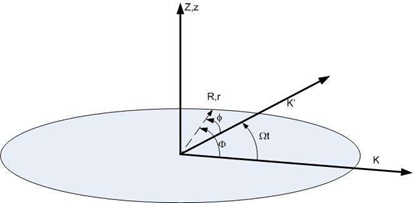
Figure 1: Centrally rotating frame of reference

The Maxwell equations in the inertial frame are:
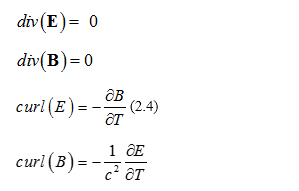 The above can be written, in cylindrical coordinates, according to (2.3) as:
The above can be written, in cylindrical coordinates, according to (2.3) as:
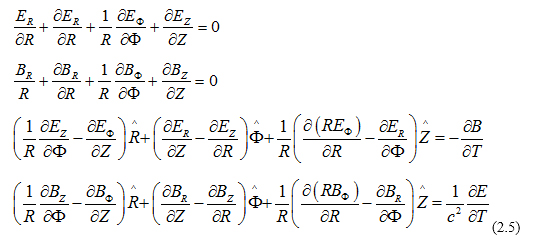 The last two equations, written on a component by component basis, become:
The last two equations, written on a component by component basis, become:
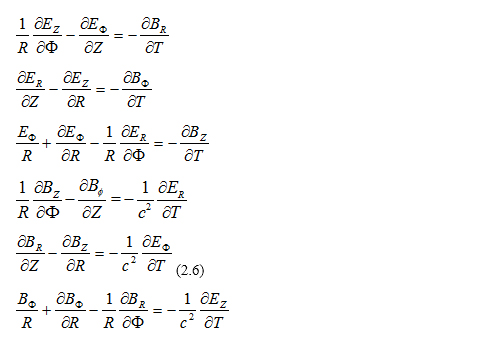 Combining (2.5),(2.6) with (2.2) we get the Maxwell equations in the rotating frame:
Combining (2.5),(2.6) with (2.2) we get the Maxwell equations in the rotating frame:
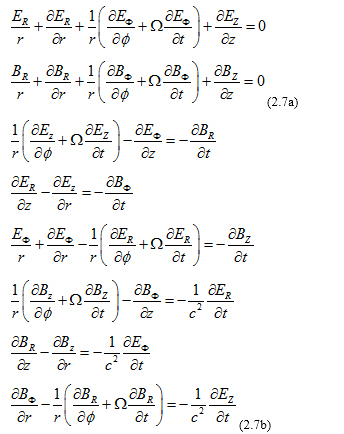 In practice, the components of the vectors E, B do not depend of coordinates, they may depend only on time, so the above equations simplify to:
In practice, the components of the vectors E, B do not depend of coordinates, they may depend only on time, so the above equations simplify to: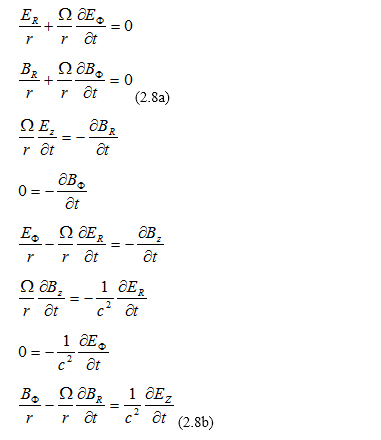 Equations (2.7a),(2.7b),(2.8a),(2.8b) mix variables from the inertial frame K and the rotating frame K’, we need to fix that. We know from the rules of vector transformation in cylindrical coordinates that:
Equations (2.7a),(2.7b),(2.8a),(2.8b) mix variables from the inertial frame K and the rotating frame K’, we need to fix that. We know from the rules of vector transformation in cylindrical coordinates that:
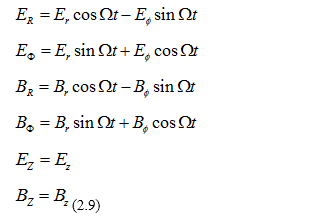 Substituting (2.9) in (2.7a),(2.7b) we get the general Maxwell equations in the rotating frame:
Substituting (2.9) in (2.7a),(2.7b) we get the general Maxwell equations in the rotating frame: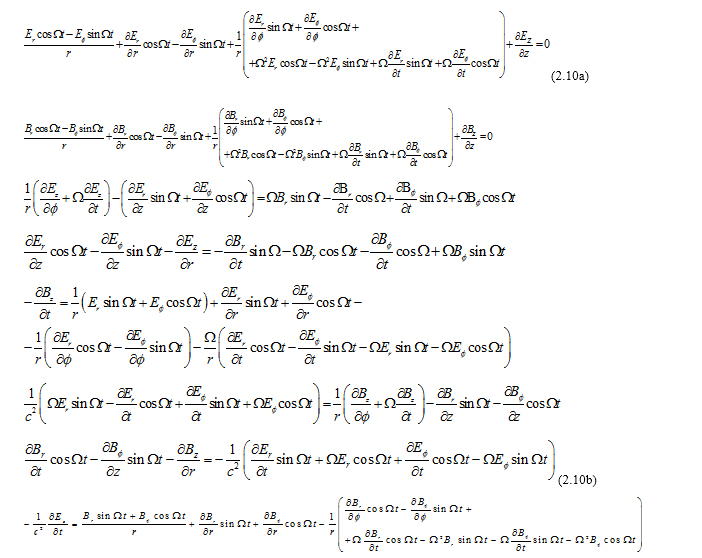 Substituting (2.9) in (2.8a),(2.8b) we get the Maxwell equations in the rotating frame for the practical cases whereby the components of the vectors E, B do not depend of coordinates:
Substituting (2.9) in (2.8a),(2.8b) we get the Maxwell equations in the rotating frame for the practical cases whereby the components of the vectors E, B do not depend of coordinates: 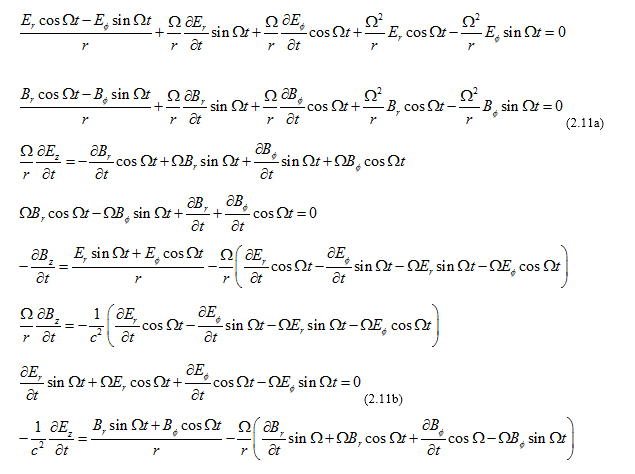
Application
Aberration and Doppler Effect of Electromagnetic Rays Propagation in a Uniformly Rotating Frame vs. the same Rays as Viewed in an Inertial Frame. Assume that in the inertial frame we have an electromagnetic wave propagating in the plane perpendicular to Z: (ER, EΦ, EZ,) = ( A Sin (ωT- K.R),0, 0) (BR, BΦ, BZ,)= (0,0, B Sin (ωT- K.Z) )
(Where K = ( K x, K y, K z ) is the wave-vector of the electromagnetic front in frame (R, Φ, Z)
Let’s Examine the Doppler Effect and electromagnetic beam aberration. This is a critical issue in the explanation of the Mossbauer rotor experiments. Let Fobs be the frequency emitted by the radiation
Source and let be the observed frequency. Let ψ be the phase of the radiation wave as measured in the inertial frame and let be the phase in the rotating frame.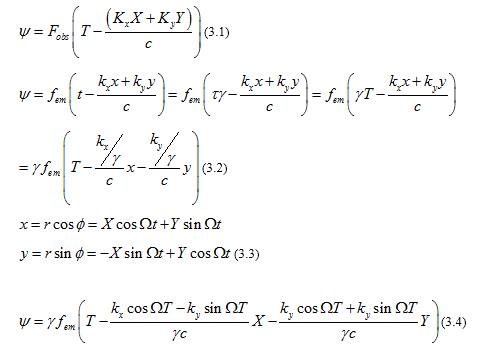 From the wave phase invariance ψ = ψ it would be naive to claim:
From the wave phase invariance ψ = ψ it would be naive to claim: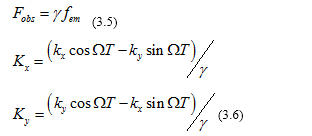 Such a conclusion is incorrect because expression (3.4) depends on T both explicitly and implicitly. Not all is lost if we consider just the particular case when the axes of the two systems of coordinates align, as in the case of the Mossbauer rotor experiments. This happens when
Such a conclusion is incorrect because expression (3.4) depends on T both explicitly and implicitly. Not all is lost if we consider just the particular case when the axes of the two systems of coordinates align, as in the case of the Mossbauer rotor experiments. This happens when 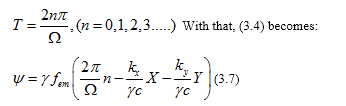
On the other hand, (3.1) becomes: 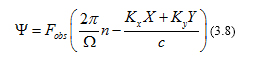
From the frame-invariance of the phase, by comparing (3.7) and (3.8) we obtain: 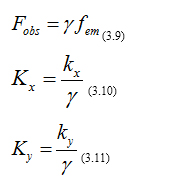
There is no aberration since the vectors (K x, K y) (k x, k y) and are collinear. An excellent confirmation of the relativistic Doppler Effect was achieved by the Mossbauer rotor experiment [9]. Gamma rays are sent from a source in the middle of a rotating disk (Figure 2) to an absorber at the rim and a stationary counter is placed beyond the absorber. The characteristic resonance absorption frequency of the moving absorber at the rim should decrease due to time dilation, so the transmission of gamma rays through the absorber increases, which is subsequently measured by the stationary counter beyond the absorber. The maximal deviation from time dilation was 10−5.Such experiments were performed by [10-13]. According to (3.9) Fobs = γfem the measured frequency is. Conversely, if the positions of the source and the absorber are swapped, the formalism developed above predicts the measured frequency to be: 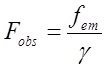 (3.12)
(3.12)
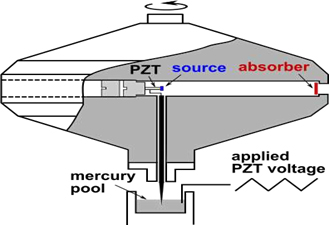
Figure 2: The Mossbauer rotor experiment
The relationship between the frequencies in the rotating frame as a function of the natural frequency in the inertial frame is, for an emitter located at distance absorber R ' from the center and the distance at R is [14,15]:
 Obviously, if R ' = R the effect is null, as observed in the Champeney experiment [16, 17].
Obviously, if R ' = R the effect is null, as observed in the Champeney experiment [16, 17].
Acknowledgment
The author wants to thank the anonymous reviewer for the valuable suggestions.
Conclusion
We have derived the Maxwell equations for the case of a rotating frame of reference. Real life applications include accelerating and rotating frames more often than the idealized case of inertial frames. Our daily experiments happen in the laboratories attached to the rotating, continuously accelerating Earth. Usually, such experiments are explained from the perspective of an external, inertial frame because special relativity in rotating frames is viewed as more complicated. We have attempted to “lift the veil” off the more mysterious rotating frames. A direct application is the formula of the relativistic Doppler Effect in the case of the emitter and absorber rotating with respect to a common center of rotation.
References
- Sfarti A (2017) Electrodynamics in Uniformly Rotating Frames the Central Observer Point of View. Theoretical Physics 2: 177-187.
- Sfarti A (2017) Relativistic Dynamics and Electrodynamics in Uniformly Accelerated and in Uniformly Rotating Frames-The General Expressions for the Electromagnetic 4-Vector Potential. IJPOT 3: 36-42.
- Sfarti A (2017) Electrodynamics in Uniformly Rotating Frames as Viewed from an Inertial Frame. IJPOT 3: 62-66.
- Hauck JC, Mashhoon B (2003) Electromagnetic waves in a rotating frame of reference. Ann Der Phys 12: 275-288.
- Mashhoon B (1989) Electrodynamics in a rotating frame of reference. PLA 139: 103-108.
- Nelson RA (1987) Generalized Lorentz transformation for an accelerated, rotating frame of reference. J. Math. Phys 28: 2379.
- Nikolic H (2000) Relativistic contraction and related effects in non-inertial frames. Phys.Rev 61: 032109-032117.
- Moller C (1960) The Theory of Relativity. Clarendon Press, Oxford.
- Kundig W (1963) Phys. Rev 129: 2371.
- Hay HJ, Schiffer JP, Cranshaw TE, Eglestaff PA (1960) Measurement of the Red Shift in an Accelerated System Using the Mossbauer Effect in Fe 57. Phys. Rev. Lett 4: 165.
- Hay HJ, Schoen A, Compton DMT (1962) in Proc. 2nd Conf, Mossbauer Effect, (NewYork: Wiley) Pg. No: 225.
- Champeney DC, Moon (1961) PB Proc. Phys. Soc.77: 350.
- Champeney DC, Isaak GR, Khan AM (1965) A time dilatation experiment based on the Mossbauer Effect. Proc. Phys. Soc85: 115-120.
- Sfarti A (2017) The Mossbauer Rotor Effect-Relativistic Electrodynamics in Uniformly Rotating Frames. IJPOT 3: 19-21.
- Sama N (1969) Some Comments on a Relativistic Frequency-Shift Experiment of Champeney and Moon. American Journal of Physics 37: 832.
- Sfarti A (2019) Special relativity experiments explained from the perspective of the rotating frame. MPLA 34: 31.
- Mossbauer RL (1958) Journal of Physics 151: 124 -143.
Citation: Sfarti A (2021) Maxwell Equations and Light Propagation in Rotating Frames. J Light Laser Curr Trends 3: 07.
Copyright: © 2021 Sfarti A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

