Non Monte Carlo Method for Intrinsic Investigation of the Potential Use of Modified Uniformly Redundant Arrays (Muras) Coded Apertures for Early Breast Tumor Imaging
*Corresponding Author(s):
Alnafea MADepartment Of Radiological Sciences, College Of Applied Medical Sciences, King Saud University, Saudi Arabia
Tel:9661-46-77-580,
Email:alnafea@ksu.edu.sa
Abstract
This is a continuous investigation of a possible application of Coded Aperture (CA) for breast tumor imaging. This paper describes a novel non-Monte Carlo method that based on a simple attractive approach called Binary Mask Shift (BMS) representing the action of a distributed source in the projective CA imaging geometry. It allows investigating all the possible built in artifacts without the effect of solid angle. Such approach allows the users to investigate all the possible built in artifacts without the effect of solid angle i.e. Ω(ro→.rm→)) r term to demonstrate the intrinsic effect of the CAs patterns. Thus, it provides understanding of the application of CAs patterns through the evaluation of their potential and their performance under a variety of imaging conditions. This may be highly attractive for certain key applications where point-like sources are to be detected, such as in early stage cancer imaging. One of the possible methods for investigating the applications of CAs for breast tumor/lymph node imaging, as an example application, is to introduce a method that represents the action of a distributed source, as found in nuclear medicine imaging, in the projective CAs imaging geometry. This approach demonstrates that MURAs and No Two Holes Touching (NTHT) MURAs CAs patterns of squares arrays are promising candidates for use in Scintimammography (SM), producing optimal decoded images (i.e. its correlation point spread function PSF produces flat (zero) side-lobes in their response function). Consequently, the technique is attractive for imaging small isolated sources and thus provides a good match to the imaging of objectives Scintimammography(SM).The main results demonstrate that MURAs patterns of squares arrays are very promising as it produces excellent decoded images. As well as this image formation allows a high photon transmission, image magnification and thus, attractive for early breast tumor imaging.
Keywords
Binary mask shift; Coded Aperture; Gamma camera; Scintimammography
Introduction
The idea of replacing the conventional collimator used in nuclear medicine imaging application by a CA was first employed by Barrett [1]. It involves the placement of a pattern of open and closed holes, forming the aperture between the source and the detecting device. Sources at different depths and positions cast a shadow (pattern) of the aperture onto the imaging detector (Figure 1). Thus, the projected image, called a composite or multiplexed image represents the sum of all projections at different x, y positions and depths within the object. To locate the proper size and position of the desired objects, the projected image must be decoded by determining the correlation of the mask pattern in size and position [2]. One of the main current applications of CA is in astronomy for stellar γ-ray and X-ray imaging [3]. There are several geometrical in near-field arrangements that can be used for CA imaging (Figure 2). For the particular application of breast imaging using nuclear medicine imaging techniques, often referred to as SM. The breast will be smaller than the detector particularly when considering a full size clinical gamma camera, and therefore the second CA camera arrangement (b), were examined. This geometry allows a basic mask pattern to be projected onto the imaging detector. However, there are physical constraints imposed by the use of a standard clinical gamma camera, wherein there is a trade-off between the maximum distance between the object and the CA mask, the size of the object or the FoV and the chosen image magnification. The latter is limited by the size of the object and more importantly by the size of the detector and its resolving capability. Several masks have been investigated in this study; 41×41 MURA (Symmetric mask) and 82×82 NTHT-MURA. It is worth noting that the smaller the CA-hole the higher the intrinsic image resolution, but this reduces geometric efficiency so that fewer photons reach the detector. In this study aperture, sizes of 2 mm and 1 mm will be examined because it may be difficult in practice to locally design aperture-holes smaller than 1 mm.
The image formation geometry and theory of MURA CAs described in these references [4-7]. This geometric theory suggest that it is possible to calculate the projection from any aperture and object based on purely geometrical calculations. It also demonstrates that the photon distribution D recorded at the detector position rl→ and due to the point source at ro→ is equal to the source (ro→) , modulated by the mask transmission A. In far-field geometry cos3(θ) ≅ 1. i.e. all photon reached parallel to the imaging detector.The last two decades have seen large efforts by scientists to develop advanced imaging instrumentation dedicated for imaging breast cancers and diseases to aid and complement the conventional method. However, this proposed method is an attractive approach as it is simple, inexpensive and the CAs has an open area significantly greater than the use of conventional collimator (Figure 1).
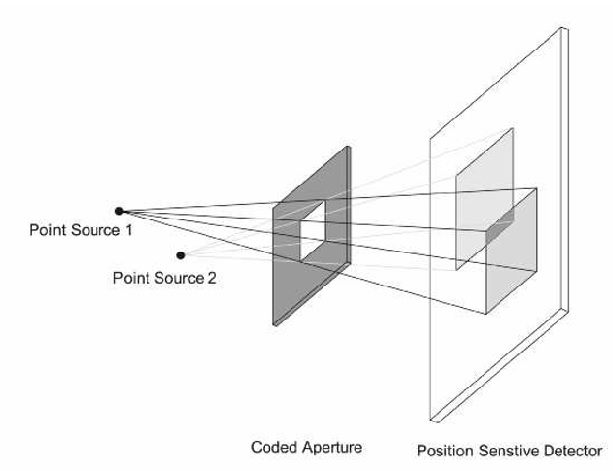 Figure 1: Schematic diagram of a CA, the production of a coded image and implicit depth information. Increasing the source-aperture distance produces a smaller shadow of the CA on the detector. The lateral displacement of the shadow is proportional to that of the two sources (source plane).
Figure 1: Schematic diagram of a CA, the production of a coded image and implicit depth information. Increasing the source-aperture distance produces a smaller shadow of the CA on the detector. The lateral displacement of the shadow is proportional to that of the two sources (source plane).
In addition, the aperture itself is employed as a simple mask so that no collimation is used, thus providing, potentially, very high sensitivity compared with the parallel-hole collimator. In the last two decays, a number of attempts have been made to use URA-CAs for 3D (SPECT and PET) imaging [8-9]. They have demonstrated that the use of URAs have improved sensitivity and resolution over single pinhole collimators. However, their resolution does not exceed that of planar parallel-hole collimators and this may be due to the complexity of the reconstruction or convolution algorithms for complex 3D imaging. To the best of the author’s knowledge, no research has systematically investigated the application of CA for planar SM except initial investigation by authors [10-11]. This paper thus, aims to examine and investigate the state of CA imaging and develops some of the theory of its application to breast tumors imaging. The main advantages of this proposed approach, is that a standard clinical gamma camera is utilized that combines image quality, affordability and ease of use and potentially reduces the need for dedicated breast camera instrumentations. This is an attractive option for health care providers with limited resources where investment in single-application dedicated instrumentation is unattractive. The major anticipated advantages and motivations are CAs imaging is well suited for detecting faint pseudo-point like objects in non-zero background. Imaging point-like small lesions (objects) in medicine is akin to imaging stellar points (objects) in astronomy. Thus, CA imaging appears well matched to the imaging objectives in SM (Figure 2).
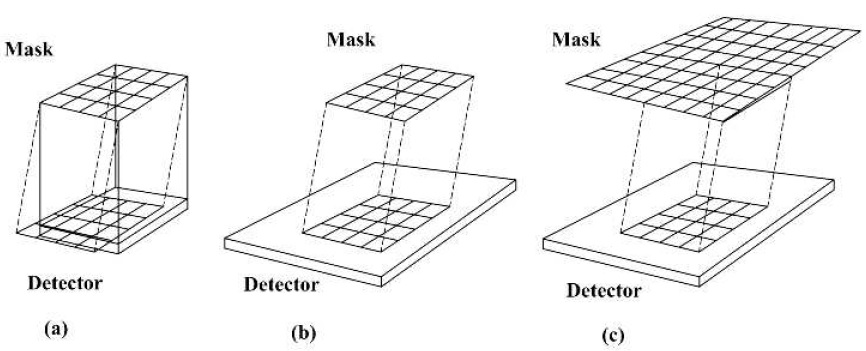 Figure 2: The three possible mask camera configurations: (a) both the mask and the camera have the same size, (b) the detector is larger than the mask; (c) The mask (2×2 mosaics of the basic pattern) is larger than the detector. These schematic diagrams are adapted from [9].
Figure 2: The three possible mask camera configurations: (a) both the mask and the camera have the same size, (b) the detector is larger than the mask; (c) The mask (2×2 mosaics of the basic pattern) is larger than the detector. These schematic diagrams are adapted from [9].
|
The Mask |
A |
B |
C |
|
Mask pattern |
MURA 41×41 |
NTHT MURA 82×82 |
MURA 31×31 |
|
Open fraction |
50% |
12.50% |
50% |
|
Mask symmetry (Fig. 3) |
Symmetric |
Anti symmetric |
Anti symmetric |
|
Mask pixel size |
2 mm |
1 mm |
2 mm |
|
Magnification coefficient |
4 |
4 |
4 |
|
Geometric resolution |
2.6 mm |
1.6 mm |
2.6 mm |
|
FoV |
8.2 cm |
8.2 cm |
6.2 cm |
|
Mask thickness |
1.5 mm |
1.5 mm |
Perfect |
Table 1: The main parameters for the masks used geometry in CA imaging investigations. All the investigation based on binary masks.
Materials &Methods Of Binary Mask Shift
Mertz and Young [12] proposed the first form of a viable CA pattern. It was used for imaging faint stars in astronomy. In such imaging application, the problem is characterized by far field geometry i.e. the objects are considered located at infinity from the detector. In this, case all photon travel in an almost parallel direction to one another as they approach the imaging detector. In the early days of this application, the Fresnel Zone Plate (FZP) pattern [12] was the most widely used CA. The early-proposed CAs imaging techniques such as the FZP [12] and the random array [13-14] have been avoided in this study. This is because these patterns fail to deliver superior results compared to collimators and pinhole camera systems, due to intrinsic distortion artifacts [15-16]. However, the development of CA patterns based on ”Cyclic Difference Sets” such as Uniformly Redundant Arrays (URAs) [6-7], Modified Uniformly Redundant Arrays (MURAs) [17] and arrays based on MURAs such as No-Two-Hole-Touching (NTHT) MURA [18-19] have been demonstrated to be the most promising of all the CA patterns. These optimum arrays as originally developed and extended by Fennimore and Cannon [2-6] [7-20] have become widely used in the detection of X-ray and γ-ray sources in astronomy for imaging stars and in nuclear medicine for small animal imaging [21]. These arrays combine high transmission characteristics, having up to 50% open area, with flat (zero) side-lobes in their response function. The high transmission provides a potential capability to image low-contrast sources and thus, dramatically enhances the detection efficiency compared to collimators system. These patterns have an interesting property that one can generate the mask and its negative (anti-mask) along with the decoding patterns, G function, for each selected binary mask. Two separate images can be then taken one with the mask and the second with the anti-mask and then add these two images after decoding each projected image with its post-processing decoding array. This technique is of special interest in artifact reduction and used in the past for reducing systemic non-uniform background [22]. Certainly, these advantages and properties have motivated the author to select this family of CA patterns as appropriate for use in this study. Several geometrical configurations considered in this study. In additions, a number of investigations carried out using 31×31 MURA (anti-symmetric mask) and 41×41 MURA masks as can see in (Figure 3). The main parameters of these masks summarized in (Table 1).
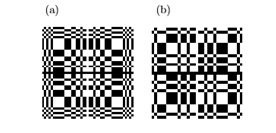 Figure 3: Two MURA patterns: (a) 41×41 symmetric mask, (b) 31×31 anti-symmetric.
Figure 3: Two MURA patterns: (a) 41×41 symmetric mask, (b) 31×31 anti-symmetric.
The BMS was initiated using the projected image array of a perfect MURA (or pattern based on MURA) binary mask generated by an on-axis point source. Then using assumed knowledge of the shape of the distributed source to be imaged, the projected pattern was systematically shifted according to the projected point source pattern that would be obtained by every non-zero element in the object. The result of each single or "binary shift" of the projected pattern is then summed with the preceding projection pattern. For illustration consider a binary mask that has been first shifted to the left then right and then up and down and finally summed [23].
 The summed shifted copies were then decoded with the usual post-processing, G function (an inverse filter of A). This binary mask displacement method represents a far-field approximation and is given by using (Eq.2) but with a constant (Ω (ro→ , rm→) ) term (Eq. 3). This noise-less composite method used to demonstrate the effect of artifacts from planar objects or displaced (shifted) sources. Mask transparency, finite mask thickness and statistical noise not considered in this approach. However, the projection data were convolved with a 2D Gaussian of standard deviation, σ= 1.57 mm, to simulate the intrinsic PSF blurring of the gamma camera. This simple BMS approach used to predict the source and the background pattern produced by uniform 2D object [23]. In more details see to (Figure 4).
The summed shifted copies were then decoded with the usual post-processing, G function (an inverse filter of A). This binary mask displacement method represents a far-field approximation and is given by using (Eq.2) but with a constant (Ω (ro→ , rm→) ) term (Eq. 3). This noise-less composite method used to demonstrate the effect of artifacts from planar objects or displaced (shifted) sources. Mask transparency, finite mask thickness and statistical noise not considered in this approach. However, the projection data were convolved with a 2D Gaussian of standard deviation, σ= 1.57 mm, to simulate the intrinsic PSF blurring of the gamma camera. This simple BMS approach used to predict the source and the background pattern produced by uniform 2D object [23]. In more details see to (Figure 4).
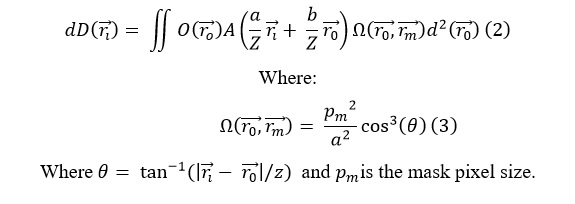
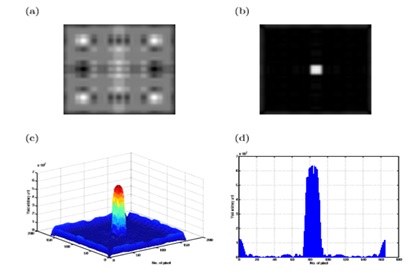 Figure 4: Exemplar plot of synthetic BMS equivalent to 1×1 cm2 square source: (a) the projected image, By correlating the recorded image with a post-processing, G function, an image of the source distribution at different depths may be determined. Note that this simple CAs pattern shown is only for illustration, as real CA designs are far more sophisticated (b). The decoded image, (c) a 3D plot of the decoded image, and (d) a vertical profile taken through the center of the decoded image.
Figure 4: Exemplar plot of synthetic BMS equivalent to 1×1 cm2 square source: (a) the projected image, By correlating the recorded image with a post-processing, G function, an image of the source distribution at different depths may be determined. Note that this simple CAs pattern shown is only for illustration, as real CA designs are far more sophisticated (b). The decoded image, (c) a 3D plot of the decoded image, and (d) a vertical profile taken through the center of the decoded image.
Results & Discussion
Theoretically, the selected CA patterns shown in (Figures 5, 3a&3b) have a wide-open area and thus about 12.5% and 50% respectively of the incident γ-rays transmitted. This may dramatically improve the photon collection efficiencies and thus may reduce the acquisition time of the imaging system compared to a collimator-based system. Combining CAs using geometric magnification with a full size standard γ-camera [25] for imaging a relatively small organ such as breast has a potential ability to maintain the resolution compared to using a conventional collimator. In addition, in practice the whole size of the mask can be chosen to be 1 mm or smaller dominates the spatial resolution, making the CA-camera very attractive for early breast tumor imaging. Ultimately, high resolution could be achieved without the need for dedicated high-resolution γ-camera instrumentations. In CA imaging, photons impinging at a wide variety of angles usually accepted, compared to the restricted angular acceptance when using collimator. This is because each hole of the CA provides a different view of the source object [10-11]. Thus, inherent depth information contained in the data that can be used to reconstruct a particular depth in the source object. This achieved by re-scaling the magnifiation factor to the desired depth. This gives 3D information (limited angle tomography) from a single conventional 2D image. Displacing the gamma camera away from the breast may allow access to a larger FoV. Thus, one possible application of CA-SM may be determining lymph node involvement. In addition, this may help in monitoring the tumor response to chemotherapy and may be used for post-surgery and post chemotherapy applications.
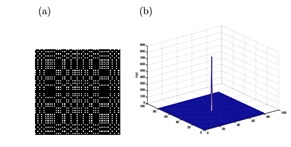 Figure 5: NTHT array of 82×82 elements and its response function: (a) NTHT array obtained from MURA pattern of size 41×41, (b) The correlation function of the NTHT-MURA demonstrating a delta function with zero side lobes.
Figure 5: NTHT array of 82×82 elements and its response function: (a) NTHT array obtained from MURA pattern of size 41×41, (b) The correlation function of the NTHT-MURA demonstrating a delta function with zero side lobes.
(Figures 6 and 7) demonstrate that the intrinsic response function image of a MURA mask of 41×41 pattern is seriously affected by the small difference in the α value. It is worth noting that in all these different data the decoding performed in the same depth. Thus, focusing the CA camera properly and decoding at the right depth minimizes these out-of-focus artifacts. As it has been suggested [16], the out-of-focus artifactsbelieved to be due to the imperfect sampling of the projected shadow. This explained considering the mask used here composed of a square array of 41×41 (p×q) elements.
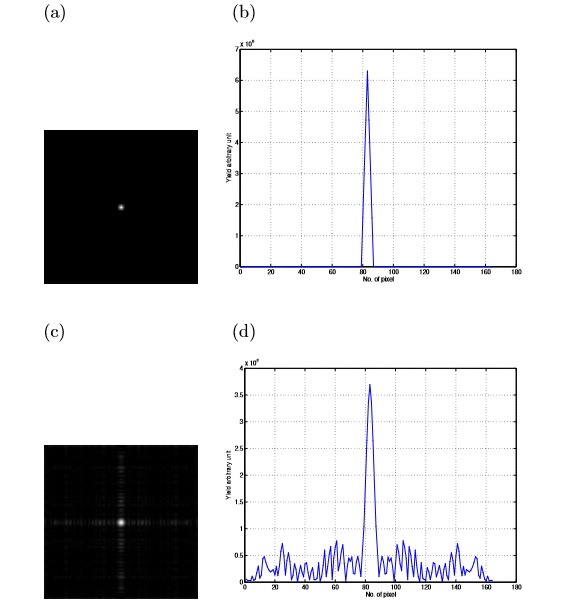 Figure 6: The effect of non-integer value of α on the PSF of a point source projected using BMS: (a) the decoded image for α=4 showing the ideal case of PSF, (b) a profile through the center of such decoded image, (c) the decoded image for α=3.9, (d) and a vertical profile through the center of the decoded image. This demonstrate that small change in α is responsible for the loss in the peak value of (b) by ≈ 42%. Note that the mean side-lobe is ≈ 0.5×108.
Figure 6: The effect of non-integer value of α on the PSF of a point source projected using BMS: (a) the decoded image for α=4 showing the ideal case of PSF, (b) a profile through the center of such decoded image, (c) the decoded image for α=3.9, (d) and a vertical profile through the center of the decoded image. This demonstrate that small change in α is responsible for the loss in the peak value of (b) by ≈ 42%. Note that the mean side-lobe is ≈ 0.5×108.
Similarly, the detector is divided into pixels but not necessarily equal to the size of the mask pixels. The projection of each hole in the aperture sampled as α×α set of the square pixels depending on the magnification coefficient (mc). This leads to an important equation that relates mc to the projection of the mask-hole [5] as in Equation 4:
α=(mc pm) /pd
Where pm represent the mask element size and pd is the size of the detector pixel. The above equation suggests that if α is integer then the projection of a point source covers exactly a square of α×α pixels. This will then provide a perfect reconstructed image. This only exists for a specific position of the point source in the object and in practice this not the case. Thus, in the case, the mask projection not matching the detector pixel i.e. α is having non-integer value then the constructed image is affected and the undesirable artifacts appear in the image. The severity of the artifacts increases as the matching of the projection and the detector pixel decreases. To investigate the effect of non-integer values of α in the decoded image, a BMS method used. Such method used to eliminate the near-field and the statistical noise effect. This work is to investigate the performance of the intrinsic response function image of a point source in air as a function of depth i.e. to carefully investigate the "depth of focus"(Figure 7). From the above investigations, one may draw and conclude that the MURA pattern for imaging a point-like object in the near field geometry has good performance with zero side lobes. However, image artifacts are intrinsic to CAs imaging when using near-field geometry even when imaging small point like objects. This BMS developed for performing the CA imaging investigations and used as the basis for artifact prediction and correction (Figure 8). One of the key results from developing this approach is that the form of the background artifact arises mainly due to the 2D distributed source geometry. In practice for slightly compressed breasts (6 cm compression), there are only minor contributions to the distributed activity artifact from depth dependent activity[23].From the above investigations one can infer that all sources at a particular depth are decoded correctly, but all others, outside this focal plane, are not, and therefore may contribute artifacts to the focal plane image. This suggests that for SM applications, where point-like objects are anticipated, it may be possible to apply a set of scaled decoding steps to seek out limited depth information as one can expect to see the highest intensity at the correctly decoded depth, dependent on the noise in the actual data. From the above discussion one can see that the post-processing array (G function) must be scaled so that it match the dimensions of the projected image. This is necessary to produce a perfect reconstructed image as imperfect matching distorts the resulting response function image (Figure 7).
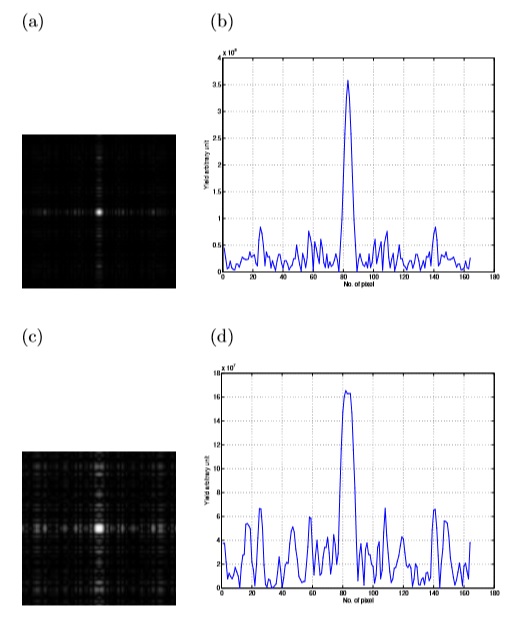 Figure 7: The effect of non-integer value of α on the response function of a point source projected using BMS method: (a) the decoded image for α=4.1. (b) A profile through the center of such decoded image showing that the small change in α is responsible for the loss in the peak value by≈ 43% compared with (Figure 6) (b). In addition, the mean side-lobe is 0.5×108. (c) The decoded image for α=4.2 and, (d) a profile through the center of such decoded image. Similarly, the loss in the peak value is ≈75%. The mean side-lobe is ≈ 0.5×108.
Figure 7: The effect of non-integer value of α on the response function of a point source projected using BMS method: (a) the decoded image for α=4.1. (b) A profile through the center of such decoded image showing that the small change in α is responsible for the loss in the peak value by≈ 43% compared with (Figure 6) (b). In addition, the mean side-lobe is 0.5×108. (c) The decoded image for α=4.2 and, (d) a profile through the center of such decoded image. Similarly, the loss in the peak value is ≈75%. The mean side-lobe is ≈ 0.5×108.
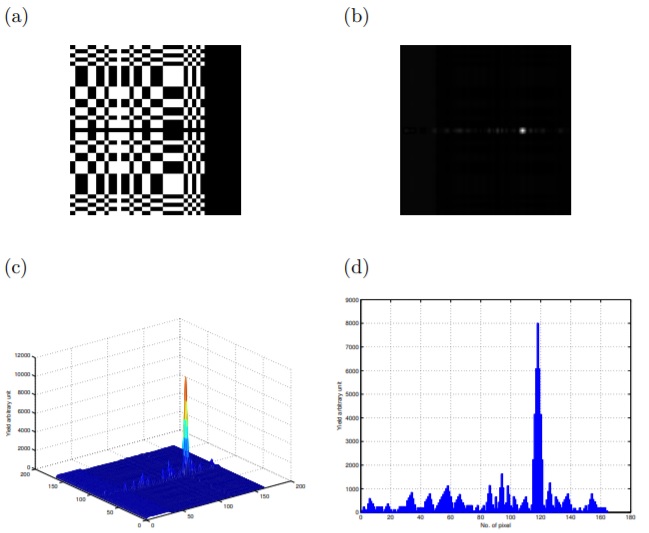 Figure 8: Exemplar plots of the BMS displaced by 3 cm: (a) shifted binary mask, (b) the corresponding decoded image, (c) a 3D plot of the decoded image and finally (d) a horizontal profile through the decoded image. This demonstrates the intrinsic imaging properties of the MURA mask.
Figure 8: Exemplar plots of the BMS displaced by 3 cm: (a) shifted binary mask, (b) the corresponding decoded image, (c) a 3D plot of the decoded image and finally (d) a horizontal profile through the decoded image. This demonstrates the intrinsic imaging properties of the MURA mask.
Conclusion
CAs imaging systems possess high photon transmission, image magnification and to a lesser extent the (limited-angle) tomographic capability. The URAs and MURAs CAs patterns possess have attractive features providing a delta-like autocorrelation function. These properties have attracted researcher in nuclear medicine imaging particularly in SM application. The non-Monte Carlo methods i.e. the BMS method [24] successfully predict the form of artifacts, in term of the shape and the magnitude of the side-lobes that is due to the off-center source displacement. Thus, by even removing the effect of varying the incident γ-ray or solid angle effect (when using the BMS method), the artifacts are still present in the decoded image. These artifacts accounted for the effect of source displacement result in losing information by not covering the whole image. This suggests that for high-resolution near-field imaging one ideally needs a large detector that fully samples the mask patterns for all the sources within the FoV. This paper investigates the CA imaging approach to be latter applied to the particular case of SM by employing 3D pseudo-anthropomorphic phantom geometries modeled. The developed phantom contains torso, heart, breast and variable tumor sizes. The recent advances in near-field artifacts correction have attracted the author to continue investigate the CA imaging technique.
Future Work
Future work will demonstrate how the selected MURA CA camera, using a standard full size clinical gamma camera, can be applied experimentally for SM application. For these investigations, pseudo-anthropomorphic phantom geometries will first developed and verified in order to emulate SM. This 3D phantom contains breast and variable tumor sizes. The influence and the contribution of out-of-field tracer uptake from other soft tissue will also investigate.
Acknowledgment
This Project was funded by the National Plan for Science, Technology and Innovation (MAARIFAH), King Abdul-Aziz City for Science and Technology, Kingdom of Saudi Arabia, Award Number (2516).
References
- Barrett HH (1972) Fresnel Zone Plate Imaging in Nuclear Medicine. Journal of Nuclear Medicine 4: 382-385.
- Cannon TM, Fenimore EE (1979) Tomographical Imaging Using Uniformly Redundant Arrays. Applied Optics 18: 1052-1057.
- Palamer D, Prince TA (1987) A laboratory demonstration of high resolution hard X-ray and γ-ray imaging using a Fourier transform techniques. IEEE Transaction in Nuclear Science 34: 71-75.
- Accorsi RF, Lanza RC (2001) Near-Field artifact reduction in coded aperture imaging. Applied Optics 40: 4697-4705.
- Jiang S, Wu Z, Ma T, Jin Y (2004) Design of Coded Aperture Collimator for High resolution & High sensitivity MicroSPECT. Conference Record Nuclear Science Symposium and Medical Conference.
- Fenimore EE, Cannon TM (1977) Uniformly redundant arrays. Proceeding Digital Signal Processing Symposium 6: 479-493.
- Fenimore EE, Cannon TM (1978) Coded aperture imaging with uniformly redundant array. Applied Optics 17: 337-347.
- Gemmill PE, Chaney RC, Fenyves EJ (1995) Monte-Carlo simulation of a coded aperture SPECT apparatus using uniformly redundant arrays. Imaging detectors in high energy and astroparticle physics: 81-115.
- Zhang L, Lanza RC, Horn BKP, Zimmerman RE (1998) Three-dimensional coded aperture techniques in diagnostic nuclear medicine imaging. SPIE Conference on Physics of Medical Imaging 3336: 364-373.
- Alnafea MA, Wells K, Spyrou NM, Saripan MI, Guy M, et al. (2006) Preliminary results from a Monte Carlo study of breast tumour imaging with low energy high-resolution collimator and a modified uniformly-redundant array-coded aperture. Nuclear Instrument and Method A 563: 146-149.
- Alnafea MA, Wells K, Spyrou NM, Guy M (2007) Preliminary Monte Carlo study of coded aperture imaging with a CZT gamma camera system for scintimammography. Nuclear Instrument and Method A 573: 122-125.
- Mertz L, Young NO (1961) Fresnel Transformation of Image. Proceeding International Conference Optical Instrumentation: 305-312.
- Dicke RH (1968) Scatter-hole Cameras for X-rays and gamma Ray. Astro-physical Journal, 153: 101-106.
- Ables JG (1968) Fourier transform photography: a new method for X-ray astronomy. Proceeedings of the Astronomic Society of Australia 1: 172-173.
- Webb S (1988) The Physics of Medical Imaging. Institute of Physics Publishing, Bristol and Philadelphia.
- Barrett HH, Swindell W (1981) Radiological imaging: the theory of image formation, detection and Processing. London, Academic Press Inc.
- Gottesman SR, Fenimore EE (1989) New family of binary arrays for coded aperture imaging. Applied Optics, 28: 4344-4352.
- Alnafea AM (2018) A Review of Coded Aperture Families having Perfect Mathematical Imaging Properties used for Near Field Imaging Application. Asian J Med Health Res 3: 07.
- Fenimore EE, Cannon TM (1981) Uniformly redundant arrays: digital reconstruction methods. Applied Optics 20: 1858-1864.
- Fenimore EE (1978) Coded aperture imaging: predicted performance of uniformly redundant array. Applied Optics 17: 3562-3570.
- Meikle SR, Fulton RR, Eberl S, Dahlbom M, Wong K, et al. (2001) An investigation of coded aperture imaging for small animal SPECT. IEEE Transactions on nuclear science, NS-48 3: 816-821.
- Dunphy P, McConnell M, Owens A, Chupp E, Forrest D (1989) A balloon-borne coded aperture telescope for low-energy gamma-ray astronomy. Nuclear Instruments and Methods in Physics Research Section A 274: 362-379.
- Alnafea MA, Wells K, Spyrou NM, Guy M (2006) A Near Field Correction for Coded Aperture Imaging in Scintimammography. Conference Record on 2006 Nuclear Science Symposium and Medical Conference.
- Alnafea MA, Mahboub D, Wells K (2017) Non-Monte Carlo Methods for Investigating the Application of Coded Aperture Breast Tumour Imaging. J Cancer Sci Thera 9: 12.
- Alnafea MA, Wells K (2018) Monte-Carlo Simulation of Infinia Gamma Camera: A Verification and Validation Process” Nessa J Cancer Sci and Therapy 1: 1-14.
Citation: Alnafea MA, Non Monte Carlo Method for Intrinsic Investigation of the Potential Use of Modified Uniformly Redundant Arrays (Muras)Coded Apertures for Early Breast Tumor Imaging (2021) J Nucl Med Radiol Radiat Ther 6: 29.
Copyright: © 2021 Alnafea MA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.