
Special Relativity Optical Experiments Explained from the Perspective of a Peripherally Rotating Frame
*Corresponding Author(s):
Adrian SfartiCs Department, University Of California, 387 Soda Hall, Berkeley, United States
Email:egas@pacbell.net
Abstract
In the current paper we present an explanation of several fundamental tests of special relativity from the perspective of the frame co-moving with a rotating observer. The solution is of great interest for real time applications because Earth-bound laboratories are inertial only in approximation. We present the derivation of the Sagnac, Michelson-Morley, Kennedy-Thorndike and the Hammar experiments as viewed from the Earth-bound uniformly rotating frame, that is, the frame of the laboratory where the experiment is taking place. To our best knowledge such an attempt has never been made before, possibly due to its mathematical difficulty, so no precedents exist, this is a first. The current paper brings new information in the following areas:
-new explanation of the Sagnac experiment
-new explanation of the Michelson-Morley experiment
-new explanation of the Hammar experiment
-new explanation of the Kennedy Thorndike experiment
The main thrust of the paper is to give a consistent explanation of various tests of special relativity as judged from the perspective of the rotating frame of the experimental setup. The theoretical results are shown to be consistent with the results derived for inertial frames in the specialty literature. The exact symbolic solutions are nevertheless different from the results obtained for inertial frames. This should not be surprising since the rotation actually “modulates” the proper speeds of the light wave-fronts.
Keywords
General coordinate transformations; Hammar experiment; Kennedy-Thorndike experiment; Michelson-Morley experiment; Sagnac experiment; Uniform rotation motion
PACS
03.30.+p, 52.20.Dq, 52.70.Nc
INTRODUCTION
Real life applications include accelerating and rotating frames more often than the idealized case of inertial frames. Our daily experiments happen in the laboratories attached to the rotating, continuously accelerating Earth. Usually, such experiments are explained from the perspective of an external, inertial frame because special relativity in rotating frames is viewed as more complicated. In the present paper, we will construct a straightforward explanation by applying the formalisms developed in previous work [1-6]. More exactly, we apply the formalisms derived in [1-3] to explaining the results of some of the most important tests of special relativity as viewed from the rotating frame of the lab where the experiments take place.
LIGHT SPEED IN UNIFORMLY ROTATING FRAMES




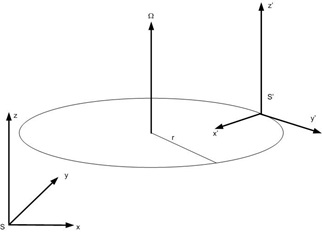
Figure 1: Peripherally rotating frame of reference.
THE SAGNAC EXPERIMENT EXPLAINED FROM THE PERSPECTIVE OF THE ROTATING PLATFORM
The Sagnac experiment [8-12] is usually explained from the perspective of an inertial frame anchored to the center of rotation since the mathematical formalism is simpler from that perspective. In this section, we will use the results derived in the previous section in order to produce an equally straight forward explanation from the perspective of a frame attached to the periphery of the rotating device. Based on the prior results, the observer co-moving with the rotating frame measures the perimeter of a circle of radius r to be 2πr, both wave-fronts cover the same distance, 2πr, so the time difference between the clockwise and counterclockwise light fronts is calculated as (absolute speeds are used):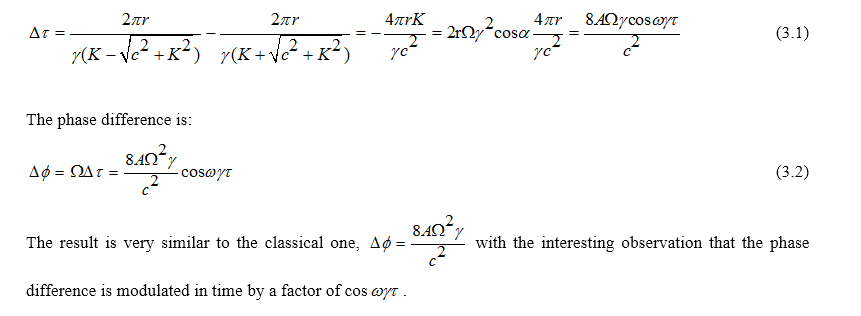
THE MICHELSON-MORLEY EXPERIMENT EXPLAINED FROM THE PERSPECTIVE OF A ROTATING EARTH-BOUND FRAME
We can now explain the null result of the Michelson Morley experiment [13-21] in the rotating frame of the lab co-rotating with the Earth. The elapsed time in the direction of motion is:
NEW EXPLANATION OF THE KENNEDY-THORNDIKE EXPERIMENT AS VIEWED FROM THE PERSPECTIVE OF A ROTATING EARTH-BOUND FRAME
The Kennedy-Thorndike experiment exploits the fact that the Earth bound laboratory has a variable speed due to the combined effect of Earth rotation around its axis and Earth revolution around the Sun [22]. The laboratory speed has contributions from the revolution of the Earth with respect to the Sun-centered frame, ve = 30km/s and Earth’s daily rotation vd so:


Once again, while the transition times in the rotating frame is different from the ones calculated for idealistic inertial frames, the measured values of the experiment are null, exactly as predicted by the above theory.
THE HAMMAR EXPERIMENT EXPLAINED FROM THE PERSPECTIVE OFA ROTATING EARTH-BOUND FRAME
In the following, all calculations explaining the outcome of the Hammar experiment [23,24] are made from the point of view of the rotating Earth-bound frame and all employ the theory of special relativity in rotating frames. The clockwise ( tcw ) and counterclockwise (tccw) time of light propagation are (Figure 2):
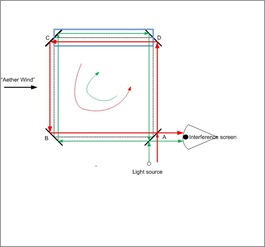 Figure 2: Instrument motion with shielded arm moving parallel to the “aether wind”. The light source as well as the screen where interference occurs between the two light beams is located in point “A”. Also, a half-silvered mirror is used as a light splitter.
Figure 2: Instrument motion with shielded arm moving parallel to the “aether wind”. The light source as well as the screen where interference occurs between the two light beams is located in point “A”. Also, a half-silvered mirror is used as a light splitter.

CONCLUSIONS
REFERENCES
- Sfarti A (2017) Electrodynamics in uniformly rotating frames the central observer point of view. Theoretical Physics 2: 177-187.
- Sfarti A (2017) Relativistic dynamics and electrodynamics in uniformly accelerated and in uniformly rotating frames-the general expressions for the electromagnetic 4-vector potential. IJPOT 3: 36-42.
- Sfarti A (2017) Electrodynamics in uniformly rotating frames as viewed from an inertial frame. IJPOT 3: 62-66.
- Hauck JC, Mashhoon B (2003) Electromagnetic waves in a rotating frame of reference. Annalen der Physik 12: 275-288.
- Mashhoon B (1989) Electrodynamics in a rotating frame of reference. PLA 139: 103-108.
- Nelson RA (1987) Generalized Lorentz transformation for an accelerated, rotating frame of reference. J Math Phys 28: 2379-2383.
- Moller C (1960) The theory of relativity. Clarendon Press, Oxford Press, United Kingdom.
- Sagnac G (1913) L’Ether lumineux demontre par l’effet du vent relatif d’ether dans un interferometre en rotation uniforme. Comptes Rendus 157: 708-710.
- Michelson A, Gale H, Pearson F (1925) The effect of the earth's rotation on the velocity of light. Astrophysical Journal 61: 137-140.
- Rizzi G, Ruggiero ML (2004) The Relativistic Sagnac Effect: two derivations. Relativity in Rotating 135: 179-220.
- Langevin P (1921) Comptes Rendus de l'Academie des Sciences (Paris) 173: 831.
- Pascoli G (2017) Comptes Rendus de l'Academie des Sciences (Paris) 18: 563.
- Michelson and Morley EW (1887) On the relative motion of the earth and the luminiferous ether. Am J Sci 34: 333- 345.
- Saathoff G, Karpuk S, Eisenbarth U, Huber G, Krohn S, et al. (2003) Improved test of time dilation in special relativity. Phys Rev Lett 91: 190403.
- Müller H, Herrmann S, Braxmaier C, Schiller S, Peters A (2003) Modern Michelson-Morley experiment using cryogenic optical resonators, Phys Rev Lett 91: 020401.
- Müller H, Herrmann S, Braxmaier C, Schiller S, Peters A (2003) Theory and technology for a modern Michelson-Morley Test of Special Relativity. App Phys B.
- Müller H, Braxmaier C, Herrmann S, Peters A, Lämmerzahl C (2003) Electromagnetic cavities and lorentz invariance violation. Phys Rev 67: 056006.
- Sfarti A (2007) Corrected Theory of the Reenactments of the Michelson-Morley Experiment in NonVacuum Media. Rom Jour Phys 52: 533-537.
- Shamir J, Fox R (1969) A repetition of the MMX with the optical paths in perspex (n = 1.49) and a laser-based optics sensitive to ~0.00003 fringe. N Cim: 2.
- Trimmer W, Baierlein R, Faller J, Hill H (1973) Experimental search for anisotropy in the speed of light. Phys Rev 8: 3321-3326.
- Trimmer W, Baierlein R, Faller J, Hill H (1974) Erratum: Experimental Search for Anisotropy in the Speed of Light. Phys Rev 9: 2489-2489.
- Kennedy RJ, Thorndike EM (1932) Experimental Establishment of the relativity of time. Phys Rev 42: 400.
- Hammar GW (1935) The velocity of light within a massive enclosure. Physical Review Journals Archive 48: 462.
- Sfarti A (2016) The Wonderful World of Hammar’s Experiment. PSIJ 12: 4.
Citation: Sfarti A (2019) Special Relativity Optical Experiments Explained from the Perspective of a Peripherally Rotating Frame. J Light Laser Curr Trends 2: 004.
Copyright: © 2019 Adrian Sfarti, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

