
Advances in Industrial Biotechnology Category: Biotechnology
Type: Short Communication
The AT -{Transmuted - X} Family of Distributions
*Corresponding Author(s):
Clement Boateng AmpaduCarrolton Road, Boston, MA 02132-6303, United States
Tel:+1 6174697268,
Email:drampadu@hotmail.com
Received Date: Feb 20, 2019
Accepted Date: Mar 07, 2019
Published Date: Mar 18, 2019
Abstract
The Exponential Transmuted Exponential distribution (ETE) appeared in and in this paper we present a new generalization of the ETE distribution based on an application of the Ampadu-G family of distributions that appeared in [1,2]. We also show the new distribution is a good fit to some real-life data, indicating practical significance. As a further development, we propose a new class of distributions based on the structure of the weight function introduced in [3].
Keywords
AT - X(W) family of distributions; Exponential Distribution; Transmuted Distribution
PRELIMINARIES
At first we recall the following definitions
Definition 1.1.
Let λ > 0, ξ > 0 be a parameter vector all of whose entries are positive, and x ? R [2]. A random variable X will be said to follow the Ampadu-G family of distributions if the CDF is given by
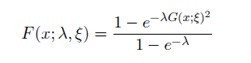
And the PDF is given by
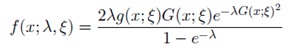
Where the baseline distribution has CDF G(x; ξ) and PDF g(x; ξ)
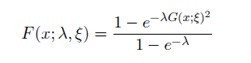
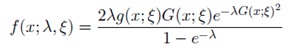
Definition 1.2.
Assume the random variable T with support [0,∞) has CDF G(t; ξ) and PDF g(t; ξ) [2]. We say a random variable S is AT - X(W) distributed of type II if the CDF can be expressed as either one of the following integrals
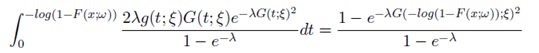
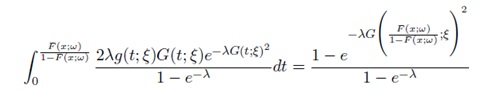
Where λ, ξ > 0, and the random variable X with parameter vector ω has CDF F(x; ω) and PDF f(x; ω)
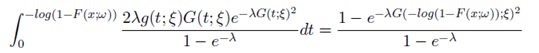
or
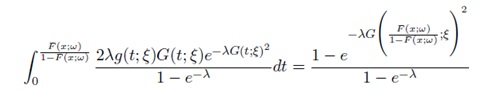
APPLICATION
As an application we consider the data on patients with breast cancer [1]. We assume the random variable T is exponentially distributed. So that the CDF of T is given by
For t, d > 0. Now we recall the following, for some baseline distribution K(x), the transmuted family of distributions has CDF given by
G(t; d) = 1 - e-dt
For t, d > 0 and the PDF is given byg(t; d) = de-dt
For t, d > 0. Now we recall the following, for some baseline distribution K(x), the transmuted family of distributions has CDF given by
(1 + b)K(x) - bK2(x)
Where b ? [-1, 1]. Now we assume X is transmuted exponentially distributed, so that ifK(x):= 1 - e-ax
For x, a > 0, then the CDF of X is given byF(x; a, b) = (b + 1) (1 - e-ax) - b (1 - e-ax)2
And the PDF is given byf(x; a, b) = a(b + 1) e-ax - 2abe-ax (1 - e-ax)
Now from the first integral in 3.2 Definition, we have the followingTheorem 2.1.
The CDF of the A{Exponential}-{Transmuted Exponential} distribution is given by
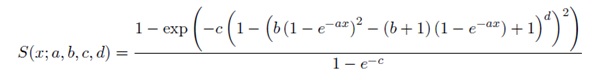
Where x, a, c, d > 0 and b ? [-1, 1]
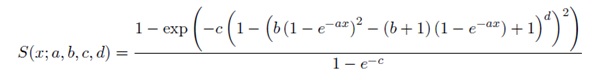
Remark 2.2.
If a random variable Q has CDF given by the above theorem, write
The AETE distribution is seen to be a good fit to real life data as shown in the figure 1.
Q ~ AETE(a, b, c, d)
The PDF of the AETE distribution can be obtained by differentiating the CDFThe AETE distribution is seen to be a good fit to real life data as shown in the figure 1.
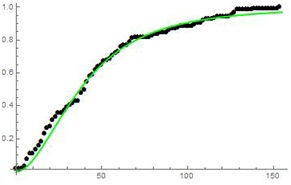
Figure 1: The CDF of AETE(0.0133756, 0.216229, 3.93753, 0.910041) fitted to the empirical distribution of the data on patients with breast cancer [1].
FURTHER DEVELOPMENTS
Inspired by the structure of the weight function introduced in, we ask the reader to investigate some properties and applications of a so-called A{New T} - X(W) family of distributions of type II [3]. We leave the reader with the following.
Definition 3.1.
Assume the random variable T with support [0,∞) has CDF G(t; ξ) and PDF g(t; ξ). We say a random variable SNew is A{New T} - X(W) distributed of type II if the CDF can be expressed as the following integral.
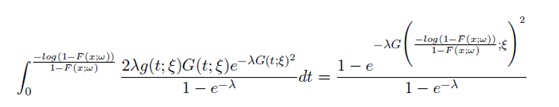
Where λ, ξ > 0, and the random variable X with parameter vector ω has CDF F(x; ω) and PDF f(x; ω)
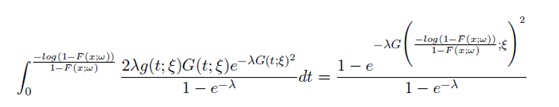
CONCLUDING REMARKS
Our hope is that the new class of distributions presented in this paper will find application in cancer modeling and forecasting
REFERENCES
- Moolath GB, Jayakumar K (2017) T-Transmuted X Family of Distributions. Statistica 77.
- Ampadu CG (2019) The Ampadu-G Family of Distributions with Application to the T-X(W) Class of Distributions. Annals of Biostatistics and Biometric Applications 1.
- Ahmad Z, Elgarhy M, Hamedani GG (2018) A new Weibull-X family of distributions: properties, characterizations and applications. Journal of Statistical Distributions and Applications 5.
Citation: Ampadu CB (2019) The AT - {Transmuted - X} Family of Distributions. Adv Ind Biotechnol 2: 006.
Copyright: © 2019 Clement Boateng Ampadu, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Journal Highlights
© 2026, Copyrights Herald Scholarly Open Access. All Rights Reserved!
