
A Dynamic Analysis of Convective Weather Using Generalized Dynamic Equations and the Scale Transformation Mechanism Related to Condensation and Freezing Processes
*Corresponding Author(s):
Xingrong WangAnhui Meteorology Institute, Anhui Key Lab Of Atmospheric Science And Satellite Remote Sensing, Hefei, Anhui, China
Email:wangxr_ahqks@yahoo.com
Abstract
To figure out the influence of non-conserved Generalized Potential Vorticity (GPV) caused by latent heating and dry diabatic heating on convective weather, a GPV equation is studied. By comparing latent heating and dry diabatic heating term with nonlinear advection term, three kinds of processes are discussed, namely adaptation, evolution, and excitation (elimination), associated with the conservative, quasi-conservative, and non-conservative GPV, respectively.
The analysis points out that:
1. Air movement transforms from smaller to larger scale by very fast adaptation process with the addition of frictional effect when the order of latent heating A and dry diabatic heating term B is lower than Rossby number R [O(f-1(A+B)/P0)<O(R)=O(W/FH)].
2. Air movement transforms from larger to smaller scale by very fast excitation process or from smaller to larger scale by very fast elimination process when the order of A+B is higher than R [O(f-1(A+B)/P0)>max(O(R),O(W/FH)].
3. Either of both kinds of scale transformation process will constantly go along till air movement is back to evolution process.
For each transformation process of convective weather, its dynamic causes, conditions and main features are theoretically analyzed and described, many puzzles about convective cloud may be understood and explained.
Keywords
Cumulonimbus; Cumulus; Generalized dynamic equations related to condensation and freezing processes; Scale transformation mechanism
INTRODUCTION
According to the traditional atmospheric dynamical equations, from Ertel H and Wu, et al., [12,13] if excluding the diabatic heating and friction, whether moist potential vorticity in relative humidity r=1 (MPV) or dry potential vorticity in r<1 (DPV), both are conservative because the solenoidal term of MPV
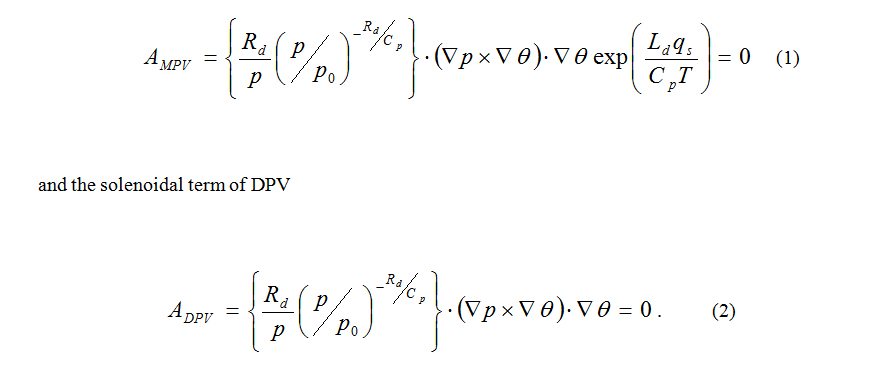
It means that all current popular research on convective weather is constrained by the conservation of potential vortices. From Wang and Huang [14], the Generalized Potential Vorticity (GPV) is found non-conservative in some very thin transitional areas. So, there are potentially useful applications of non-conservative property of the GPV in the convective storm realm that are as yet unrealized.
According to Doswell CA [15], despite the fact that there might be a layer in the atmosphere that has positive values of Convective Available Potential Energy (CAPE), if the parcel does not reach or begin rising to that level, the most significant convection that occurs in the Free Convective Layer (FCL) will not be realized. This can occur for numerous reasons. Primarily, it is the result of a cap, or convective inhibition (CIN/CINH). Processes that can erode this inhibition are heating and forcing of the Earth's surface. Such forcing mechanisms encourage upward vertical velocity, characterized by a speed that is relatively low to what you find in a thunderstorm updraft. Because of this, it is not the actual air being pushed to its FCL that ‘breaks through’ the inhibition. So it can be determined that the heating and forcing of the Earth's surface is a toggle condition, and is a necessary but insufficient condition to break CIN. In fact, discontinuity in the latent heat term is generally found upon considering the transitional areas between unsaturated and saturated air as well as air below and above the freezing point. Traditionally, discontinuity in the latent heat term is represented by the Heaviside step function (δ(0,1)) and increases the difficulty in ordinary theoretical analyses. Certain discussions are constrained by saturated air and equilibrium airflow conditions, for example, Wu, et al., (1995), Ooyama and Schubert, et al., [13,16,17].
Wang and Wu [18] introduced the condensation probability function rk(r is relative humidity) based upon the observational evidence presented by Mason [19] to represent the continuity of the variations observed in the discontinuity of the condensation latent heat term. Given that the condensation process may occur at r = 78%, Wang XR, Wang ZX, and Shi CE [20,21] observed rk is close to zero in r < 78% and rk= 1 in r = 1 when k ≈ 9. The condensation in air is well represented. Following these discussions, the dynamic equations of nonuniform saturated moist air were provided.
From the discuss of tendency equation of nonuniform saturated moist potential vorticity or Generalized Moist Potential Vorticity (GMPV), in some very thin transitional areas (sub-saturated area (0.78 < r < 1), GMPV is found non-conserved because of the introduction of the condensation probability function even in frictionless and moist adiabatic air motion [22], Based on this conclusion, the scale transformation mechanism of nonuniform saturated moist air [23] is discussed.
On the scale transformation mechanism, an examination of the non-conservation conditions of the nonuniform saturated moist potential vorticity theoretically proved four necessary occurrence conditions for sudden heavy rain (thunderstorm), which are confirmed with data [24]. Their analyses showed that the decline of the cold moist air stream above CIN can erode CIN and make ∂θ°/∂z being fast and sufficiently close to zero. It makes convective available depth (satisfying sufficient and necessary conditions of the moist excitation process) extending beyond the CIN top before it was destroyed after the CIN has eroded, once this depth extends to a deep convective depth, the thunderstorm occurs, which means that the thicker the depth of the eroded CIN is, the stronger the excited convective positive vorticity system. In fact, before the occurrence of essentially all the thunderstorm, except the heating and forcing of the Earth's surface, the cold moist air stream above the CIN has sunk, which means that it is possible to predict the time and intensity of severe convective weather based on these symptoms [24,25].
According to the above research results, it can be determined that a toggle process [the heating and forcing of the Earth's surface pushing the parcel to some very thin subsaturated area (1 > r > 0.78)] with the eroded process of CIN [the decline of the cold moist air stream above CIN] is an insufficient and necessary condition to break CIN. This also shows that the restrictions of the conservation law of the potential vortices must be broken down to make greater progress in convective weather forecasting and understanding.
The theory and application of nonuniform saturated moist air dynamics and the corresponding scale transformation mechanism on the occurrence conditions of thunderstorm has recently seen great progress. However, the difficulties in the discontinuity of the freezing latent heat term still limits the theoretical understanding and interpretation of the effect of freezing processes on convection weather.
Regarding the discontinuity of the freezing latent heat term, besides the condensation probability function [18,22], the freezing probability function is introduced into the dynamic framework based on the statistical thermodynamic fluctuation theory to derive the generalized thermodynamic equation in relation to the condensation and freezing processes [14]. “From the discussion of tendency equation of the GPV, in some very thin transitional areas [sub-saturated area ( 0.78 < r < 1 and T > 277.13K ), subfreezing saturated area ( 269.13K < T < 277.13K and r = 1) and the subfreezing and subsaturated area ( 269.13K < T < 277.13K and 0.78 < r < 1 )], GPV is found non-conserved because of the introduction of the condensation probability function and freezing probability function, even in frictionless and moist adiabatic air motion”[15].
To figure out the influence of non-conserved GPV caused by latent heating and dry diabatic heating on convective weather, the scale transformation mechanism related to condensation and freezing processes is discussed in Section 2. Followed by the discussion mentioned above, a dynamic analysis of convective weather is provided in Section 3. The conclusions are given in Section 4.
THE SCALE TRANSFORMATION MECHANISM RELATED TO CONDENSATION AND FREEZING PROCESSES
2. The elimination process is not considered when discussing non-uniform saturated moist PV non-conservation process.
For this reason, the scale transformation mechanism will be revisited. If generalized potential temperature θ* is defined as follows:


For figuring out the influence of non-conservative GPV caused by latent heating and dry diabatic heating on convective weather, according to the relativity principle of conservation, following Wang and Wei [12], using processing method similar to scale analysis, equation (7) can be expressed non-dimensionally as follows:
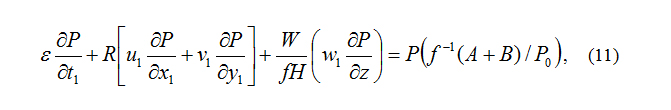
To distinguish whether there is a scale transformation process, with the aid of scale analysis, by comparing latent heating and dry diabatic heating term ( A+B ) with nonlinear advection term, following criteria can be used:

It should be pointed out that, in the case where (14) is satisfied, that is, in non-conserved GPV processes, there are two cases, A+B > 0 and A+B < 0.A has two cases: A > 0 when the gradient has a component counter to the direction of the Baroclinic vector, and A < 0 when the gradient has a component in the direction of the baroclinic vector. B also has two cases depending on distribution vector of heating or cooling field ∇q : B > 0 when ∇q > 0 and B < 0 when ∇q < 0. Therefore non-conserved GPV processes are named excitation or elimination processes.
The adaptation process
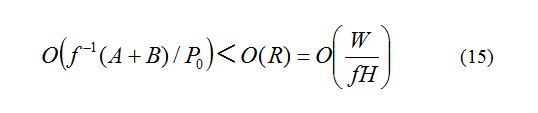
Discussions on this topic are quite mature. From Yeh and Li [27], this process is a rapid adaptation process wherein the non-equilibrium of air pressure gradient force, Coriolis force, inertial force, and gravity disappears due to the dispersion of gravity and the sound waves. This adaptation process, with the addition of frictional effect, transforms a small-scale movement into a larger scale movement, and continues until equation (15) is no longer satisfied. In reality, small to large scale transformation proceeds very rapidly, which is a rapid process. For this reason, slow nonlinear advection impacts can also be omitted in this process.
Given that (A+B)/P0 can be omitted from equation (15), this process proceeds in a closed or quasi-closed system. The system entropy increases due to the dispersion of the gravity and sound waves according to the second law of thermodynamics. Therefore, the entire system is nondissipative.
The excitation (elimination) process
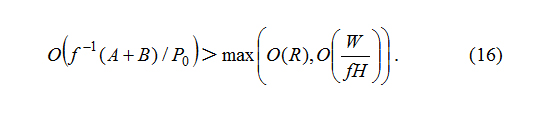

From equation (14), the temporal scale of excitation or elimination process mostly depends on the value of P0 and (A+B), which is much smaller than that of common air movement at the same spatial scale. This is also a rapid process.
When an excitation or elimination process occurs, GPV tendency equation (5) or (7) can be simplified using equation (16) as follows:

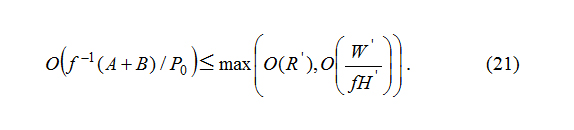
When the perturbation caused by (A+B) eliminates a convective available weather system, in which ∇P0≈0 , even though the effects of elimination and adaptation processes are the same, and both are the transform process from a smaller to a larger scale, the mechanisms are different. The elimination process is achieved by the forcing of A or B. On the contrary, the adaptation process is implemented by the dispersion of gravity and the sound waves.
The omission of the max[O(R)=O(W/fH)] in equation (14) suggests this process to be a linear process rather than a nonlinear one, and the system entropy decreases due to the excitation action of (A+B) or the system entropy increases due to the elimination action of (A+B). Therefore, it does not agree with the second law of thermodynamics. This process is in an open system, however, it is not in a thermodynamically steady state. Therefore, the entire system does not have a dissipative structure.
The evolution process
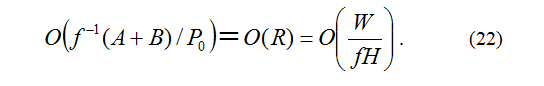
Equation (13) shows interrelation and dependence on (A+B)/P0 between the spatial and temporal scales, which suggest that (A+B), the spatial scale, and the temporal scale do not change or change slowly. Therefore, this is a slow process and is not the scale transformation process.
Equation (13) also indicates that this process is not only in an open system but is also in a thermodynamically steady state because both O(R)=O(W/fH) and (A+B) cannot be omitted. Therefore, the system entropy does not change or changes slowly due to the mutual offset of the adaptation and excitation (elimination) impacts in addition to the frictional effect, thereby presenting the entire system with a dissipative structure.
In the evolution process, (A+B), GPV, the spatial scale, and the temporal scale do not change or change slowly. However, the change in (A+B) and the nonlinear advection may make the sufficient and necessary condition of the adaptation and excitation or elimination process satisfied. If so, the corresponding adaptation and excitation or elimination process can occur.
A DYNAMIC ANALYSIS OF CONVECTIVE WEATHER
According to the conditions of excitation process [equation (16) or (17)], when A+B > 0 with P0sufficiently close to zero (P0= ζ?a.∇θ* ≅ 0 ), (A+B) can excite a weather system. In mid-latitude large-meso scale movements, ζ?a≅a a constant vector and is almost parallel to the vertical coordinate. Therefore, the above conditions can be simplified as A+B > 0 with ∂θ*/∂z sufficiently close to zero ( A+B > 0 with ∂θ*/∂z≅0). From the expression of θ*, A and B, (4), (8) and (9), the conditions of dry excitation can be simplified as (∇q > 0 with ∂θ/∂z≅0 ); the conditions of moist excitation is that the θm* gradient vector has a component counter to the direction of the baroclinic vector with θm*/∂z ≅0 ((∇p x ∇θ).∇θ* with ∂θm*/∂z≅0) and the conditions of ice excitation is ((∇p x ∇θ).∇θ* > 0 with ∂θi*/∂z≅0 ).
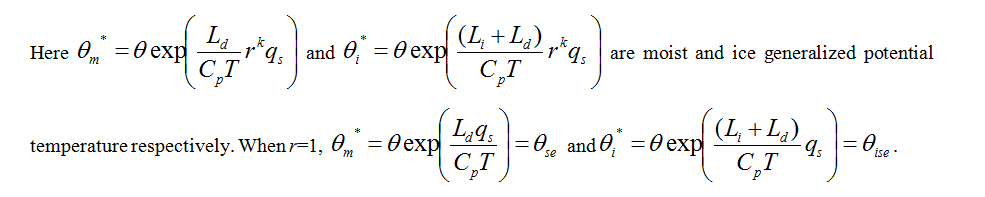
In the cumulus (Cumulus humilis and Cumulus congestus), when the rising air parcel reaches the condensation level and enters the subsaturation state, if the sufficient and necessary condition of the moist excitation process [the air in the subsaturated state, ((∇p x ∇θ).∇θ* > 0 and ∂θm*/∂z≅0 ] is satisfied, the air in the subsaturated state quickly becomes saturated and ∂θm*/∂z≅0) quickly transforms into ∂θm*/∂z=0) , so both the condensation process and a moist convective positive vorticity system (cumulus cloud) occur.
According to the scale transformation mechanism, this system exhibits an increase in GPV from Pd (GPV in the dry area) to Ps(GPV in the saturated area) coupled with rising air moving from dry areas into saturated areas through a very thin sub-saturated area at the cloud base (the green line in Figure 1). Contrarily, a decrease in GPV from Ps to Pd may be observed, coupled with rising air moving from saturated areas into dry areas through a very thin sub-saturated area at the cloud top (the green line in Figure 1a). However, in the cloud, GPV is conservative becauseθ*= θse and ∂θm*/∂z= ∂θse/∂z=0 (Figure 1a). Above the cloud top, the rising air in the sub-saturated state continues to quickly transform into the saturated state and ∂θm*/∂z≅0 continues to quickly transform into ∂θse/∂z=0 , so cumulus cloud or the moist GPV non conserved process continues to stretch and develop upward (the GPV conservative saturated area becomes higher and larger coupled with the expansion of a thin GPV non-conservative sub-saturated area), given that the condition (the air in the sub-saturated state, ((∇p x ∇θ).∇θ* > 0 and ∂θm*/∂z≅0 ) is satisfied.
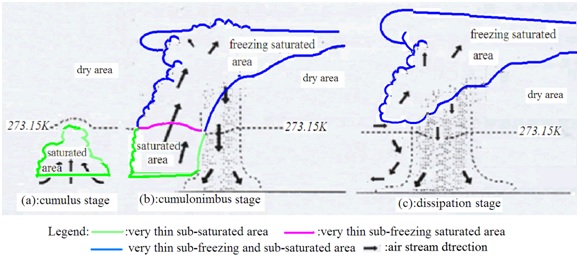 Figure 1: A schematic diagram of the dynamic analysis of convection stages.
Figure 1: A schematic diagram of the dynamic analysis of convection stages.Once the ascending height of cumulus cloud results in a temperature drops below 277.13K, according to Wang Huang [14], the satisfaction of the random temperature variable Tx≤273.15K and the condensation condition directly transforms the water vapor into solid water (deposition). That is, the freezing phenomenon with the freezing probability φ (T) appears, which begins the ice excitation process, it is, cumulonimbus occurs.
In the cumulonimbus (Cumulonimbus calvus and Cumulonimbus capillatus), as the ascending height of cumulus cloud causes the temperature T to drop below 277.13K, the ice excitation process proceeds if the sufficient and necessary condition of the ice excitation process (the air in sub-freezing saturated state or the subfreezing and sub-saturated state, ((∇p x ∇θ).∇θ* > 0 with ∂θi*/∂z≅0 ) is still satisfied above the cloud top. The air in sub-freezing saturated state or the sub-freezing and sub-saturated state is quickly becomes the freezing saturated state and ∂θi*/∂z≅0 ) quickly transforms into ∂θi*/∂z = ∂θise*/∂z = 0 ) , so both the freezing process (the water vapor with the airborne liquid water in cloud satisfying Tx≤273.15K is directly transformed into solid water) and a ice convective positive vorticity system (cumulonimbus cloud) occur. In this system, an increase in GPV from Pd to Ps is observed coupled with rising air movements from dry areas into saturated areas through a very thin sub-saturated area at the cloud base, which is similar to the moist convective positive vorticity system in the cumulus. However, above the saturated area, there is an additional increase in GPV from Ps to Psf [GPV in the freezing saturated area, (r = 1 and T < 269.13K)] coupled with rising air movement from the saturated area into the freezing saturated area through a very thin sub-freezing saturated area ( 277.13K > T > 269.13K and r = 1) near the 273.15K isothermal surface (red line in Figure 1b). There is also a correspondingly larger decrease in GPV from Psf to Pd (not from Ps to Pd ) coupled with rising air movement from the freezing saturated to dry area through very thin sub-freezing and sub-saturated area (blue line in Figure 1) at the cloud top (Figure 1b). However, in the freezing saturated area, the GPV is once again conservative because θ* = θexp((Li + Ld)qs/CpT = θise . If the sufficient and necessary condition of the ice excitation process is satisfied, the rising air in the subfreezing and subsaturated states above the cloud top continues to quickly move into the freezing saturated state. This system or cloud continues to develop upward, Cumulus congestus becomes Cumulonimbus calvus and then becomes Cumulonimbus capillatus.
At this stage, cumulus surrounding the earliest cumulonimbus will quickly merge via the convergence air stream, because
1. The additional increase of earliest cumulonimbus in GPV (from Ps to Psf through the very thin sub-freezing saturated area) makes its upward vertical velocity more powerful than any other cumulus
2. Unlike the very thin sub-saturated area, the very thin sub-freezing saturated area is close to the 277.13K isothermal surface and extends from the inner to outer regions almost horizontally. This creates an increasingly extensive early cumulonimbus.
From Wang et al, (2006) and Cheng et al, (2003)[24,25], if the upward cloud top of cumulus or cumulonimbus meets the sinking cold moist air stream from the CIN top, the rising air compels the sinking cold moist air stream to stop sinking and to rise such that the height satisfying the sufficient and necessary condition of the moist or ice excitation process can quickly extend to the original height of the sinking cold moist air stream above the CIN.
When the sufficient and necessary condition of the moist or ice excitation process is no longer satisfied, the moist or ice convective positive vorticity system returns to a new evolution process at the meso-microscale (not at large scales) and is in a thermodynamically steady state for an extended period of time. In the most vigorous stage of Cumulonimbus capillatus, the cloud top shape often becomes anvil-shaped and horizontally spread in the direction of the wind because of the inhibition of a strong stable layer above it and the impact of its upper maximum wind speed.
In addition, when cumulus or cumulonimbus is in a thermodynamically steady state, A+B≅0 with ∂θ*/∂z≅0 in very thin sub-saturated or sub-freezing and sub-saturated area of cloud but A+B≅0 with ∂θ*/∂z = 0 in cloud. If the θ* gradient having a component in (no longer counter to) the direction of the baroclinic vector, it is, (∇p x ∇θ).∇θ* > 0 (A<0) at the sub-saturated or subfreezing and subsaturated area of cloud base, from the sufficient and necessary condition of elimination process the convergence sinking airflow (caused by the decrease (instead of increase) in GPV and the occurrence of convective inverse vorticity system) will instead be observed upward from the cloud base. Once so, the convective cloud dissipation stage begins.
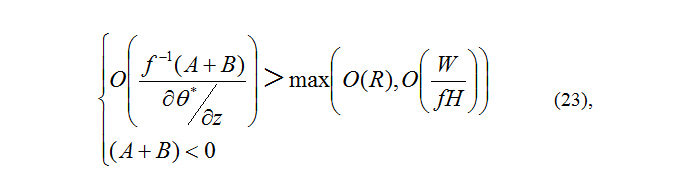
CONCLUSION
For each transformation process of convective weather, its dynamic causes, conditions and main features are theoretically analyzed and described, many puzzles about convective may be understood and explained.
A particularly important finding in the analysis suggests that cumulus surrounding the earliest cumulonimbus quickly merges via a convergent air stream during the cumulonimbus stage, which makes the cumulonimbus increasingly extensive.
The present study only offers preliminary work. In order to break down the restrictions of the conservation law of the potential vortices to make greater progress in convective weather forecasting and understanding, a lot of space and effort is still needed to perfect this huge project.
First, establish the numerical simulation models based on generalized dynamic equations related to condensation & freezing processes to confirm the dynamic causes, conditions and main features of each convective cloud pointed out in this paper.
Secondly, according to theoretical work of dynamic analysis of convective weather in this paper, design and produce charts showing the thickness of CIN and the trace process of CIN in the vertical and horizontal planes to determine the intensity, time and location of the strong convective weather that will occur.
Thirdly, according to theoretical work of dynamic analysis of convective weather in this paper, revisit convective scheme or even parameterization to improve them.
Therefore, as the beginning of the entire huge research process, due to the limitation of the thesis, our current work can only be the mathematical reasoning on one idealized figure based on the first principles.
ACKNOWLEDGEMENT
REFERENCES
- Wilson JW, Roberts RD (2006) Summary of convective storm initiation and evolution during ihop: Observational and modeling perspective. Monthly weather review 134: 23-47.
- Markowski P, Hannon C, Rasmussen E (2006) Observations of convection initiation "failure" from the 12 june 2002 ihop deployment. Monthly weather review 134: 375-405.
- Weckwerth TM, Parsons DB (2006) A review of convection initiation and motivation for ihop_2002. Monthly weather review 134: 5-22.
- Doswell CA (2007) Historical overview of severe convective storms research. E-Journal of Severe Storms Meteorology 2: 1-25.
- Gao S, Yang S, Chen B (2010) Diagnostic analyses of dry intrusion and nonuniformly saturated instability during a rainfall event. Journal of Geophysical Research: Atmospheres 115: 2.
- Wakimoto RM, Murphey HV (2010) Frontal and radar refractivity analyses of the dry line on 11 june 2002 during ihop. Monthly weather review: 138: 228-241.
- Wakimoto RM, Murphey HV (2010b) Analysis of convergence boundaries observed during ihop_2002. Monthly weather review 138: 2737-2760.
- Markowski P, Richardson Y (2011) Mesoscale meteorology in midlatitudes. Wiley?Blackwell.
- Luo YL, Gong Y, Zhang DL (2014) Initiation and organizational modes of an extreme-rain-producing mesoscale convective system along a mei-yu front in east china. Monthly weather review 142: 203-221.
- Yu XD, Zhou XG, Wang XM (2012) The advances in the now casting techniques on thunderstorms and severe convection (in Chinese). Acta Meteorologica Sinica 70(3): 311-337.
- Wang H, Luo YL, Jou BJD (2014) Initiation, maintenance, and properties of convection in an extreme rainfall event during SCMREX: Observational analysis. JGR Atmospheres 119: 13206-13232.
- Ertel H (1942) Ein neuer hydrodynamischer Wirbelsatz. Meteorolog. Zeitschr (Braunschweig) 59: 277-281.
- Wu GX, Cai YP, Tang XJ (1995) Moist Potential vorticity and up-slide vorticity development (In Chinese). Acta Meteor Sinica 53: 387-405.
- Wang XR, Y Huang (2018) Generalized dynamic equations related to condensation & freezing processes. JGR Atmospheres 123: 882-889.
- Doswell CA (2001) Severe Convective Storms-An Overview. A Meteorological Monograph, The American Meteorological Society 69.
- Ooyama KV (2000) A dynamic and thermodynamic foundation for modeling the moist atmosphere with parameterized microphysics. J Atmos Sci 58: 2073-2102.
- Schubert WH, Hausman SA, Garcia M (2001) Potential vorticity in a moist atmosphere. J Atmos Sci 58: 3148-3157.
- Wang XR, KJ Wu (1995) An approach to the dynamics of moist air (in Chinese). Sci Meteorol Sin 15: 9-17.
- Ludlam FH, Mason BJ (1971) The physics of clouds. Geophysics 479-540.
- Wang XR, ZX Wang, CE Shi (1998) On the non-conservativeness of wet potential vorticity of air motion (in Chinese). Sci Meteorol Sin 18: 135-141.
- Wang XR, Wang ZX, Shi CE (1999) The introduction of condensation probability function and the dynamic equations on non-uniform saturated moist air (in Chinese). Trop Meteorol 15: 64-70.
- Gao S, Wang X, Zhou Y (2004) Generation of generalized moist potential vorticity in a frictionless andmoist adiabatic flow. Geophysical Research Letters 31: 1211.
- Wang XR, M Wei (2007) Theoretical analysis of non-uniform saturated moist potential vorticity (The non-uniform saturated moist potential vorticity) associated with the occurrence and development of weather systems (in Chinese). J Trop Meteorol 23: 459-566.
- Wang XR, YY Zheng, ST Gao, K Zhou (2006) Possible premonitory characters of Doppler Radar product and cloud chart for the mid-latitude sudden heavy rain (in Chinese). J Trop Meteorol 22: 612-617.
- Cheng XY, Wang XR, Hu W, Wang YB (2003) On omen characteristic of thunderstorm from process on DOPPLER RADAR VWP IMAGE. (in Chinese). Sci MeteorolSin 23: 486-490.
- Lakshmi H Kantha, Carol Anne Clayson (2000) Numerical Models of Oceans and Oceanic Processes. Academic Press, London, UK.
- Yeh TC, Li MC (1965) The Adjustment Process in Atmospheric Movement (in Chinese). China Science Press pp. 1-126.
- Doswell CA (1985) The operational meteorology of convective weather. Volume II. Storm scale analysis. NOAA technical memorandum ERL ESG 15: 240.
- Emanuel (1974) Atmospheric convection. Oxford University Press, United Kingdom.
- Wang XR, Y Feng (2015) The introduction of specific water and maximum airborne specific water & the improvement of dynamic equations on non-uniform saturated moist atmosphere. ACS 5: 245-256.
Citation: Wang X, Zhou Y, Huang Y, Zhang Z (2019) A Dynamic Analysis of Convective Weather Using Generalized Dynamic Equations and the Scale Transformation Mechanism Related to Condensation and Freezing Processes. J Atmos Earth Sci 3: 009.
Copyright: © 2019 Xingrong Wang, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

