
Age, Growth and Mortality of Terapon puta (Cuvier, 1829) in the Lake Timsah, Egypt
*Corresponding Author(s):
Mohamed El-DrawanyDepartment Of Zoology, Zagazig University, Zagazig, Egypt
Email:samy_drawany@yahoo.com
Abstract
In the present study Age, Growth and Mortality of Terapon puta was estimated for 335 specimens collected by monthly sampling. This study was carried out from June 2012 to May 2013 in the Lake Timsah, Egypt. The age of Terapon puta was estimated by examining scales and it was found out that the maximum age was three years. The main total length and total weight values were calculated as 10.73±1.04 cm to 28.9±1.73 g and the calculated length-weight relationships were W = 0.023425 L2.88. The von Bertalanffy growth parameters were L∞ = 17.18 cm, K = 0.2632 year-1 and to = -1.9363 year. The instantaneous rate of total mortality (Z) was 1.49882, the natural Mortality (M) was 0.4322 and the Fishing mortality (F) was estimated to be 1.06662. The exploitation rate (E) was calculated as 0.71 using value of M and F. Therefore, the population of Terapon puta off Lake Timsah was under the threat of over fishing.
Keywords
INTRODUCTION
Terapon puta is a medium size fish which inhabits the sea in Egyptian coasts. This fish has been popular as excellent sea food with a sensible market price. Though they are not commercially important, they constitute a regular fishery throughout the year. No information available regarding the growth studies of Terapon puta with the view of supplementing this, the present study was undertaken in the Lake Timsah, Egypt.
In this study, it is expected to determine the age, growth rate, length- weight relationship and age composition of Terapon puta with von Bertalanffy growth models. Additionally, the natural and fishing mortality and the level of exploitation of this fish species off Lake Timsah were also estimated. The main aim of the present study was to shed light on some biological and dynamic features of the Terapon puta. Using such information is essential for the management and the good precision of the fishing in the lake Timsah.
MATERIALS AND METHODS
Age was determined by counting the annual rings on the scales using micrometer eye piece. In order study the time of ring formation to establish its annular nature, the scales representing rings under formation (growth checks) at the outer margin in different months were examined. To clarify further, the time of annulus formation, the distance from the last annulus to the margin of the scales were measured. A plot of monthly frequency of such scales which have marginal rings indicated the seasonal and established the annual nature.
Length-weight relationship was obtained since the total weight of each fish specimen was given with a digital balance to an accuracy of 0.01 g and total length was measured with a precision of 0.01 cm. This relationship was determined according to the allometric equation given by Sparre et al., [3] as:
W = a Lb
Where (W) is the total body weight in g, (L) is total length in cm; a and b are regression constants (Figures 1 and 2).
 Figure 1: Showing Terapon puta (12.5 cm).
Figure 1: Showing Terapon puta (12.5 cm). Figure 2: An scale from Terapon puta showing the ageing (Annual rings marked).
Figure 2: An scale from Terapon puta showing the ageing (Annual rings marked). Lt = L∞ (1 - e- k(t - to) )
Whereas (L) is the asymptotic total length, (Lt) is the total length at age (t), (k) is the growth curvature parameter and (to) is the theoretical age when fish is at zero total length. These growth parameters were estimated by means of von Bertalanffy plot Sparre and Venema [4].
Total mortality rate (Z) was estimated based on the length at first capture methods evaluated by Beverton and Holt [5].
L∞ - Lm
Z = K * (--------------)
Lm - LC
Where: Lm = The average total length of the entire catch.
LC = The length at which 50% of the fish entering the gear are retained Sparre et al., [3].
Instantaneous natural mortality rates (M) were estimated using the equation derived by Ursin [6] based on the mean total length where:
M = W–(1/b)
W = Mean total length.
b = Constant of length weight relationship.
Fishing mortality rates (F) were calculated as the difference between Z and M (Z = F + M). The value of the average annual exploitation rate (E) was obtained by E = F/Z.
RESULTS
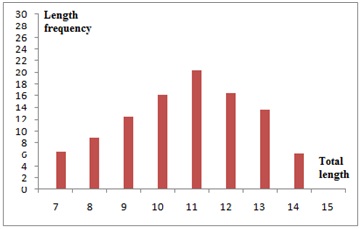 Figure 3: Length frequency distribution for Terapon puta off Lake Timsah in Egypt.
Figure 3: Length frequency distribution for Terapon puta off Lake Timsah in Egypt.The time of the annulus formation
The mean marginal growth was calculated from scales for each month in order to establish the time of annulus formation which is shown in table 2 and represented graphically in figure 4 for Terapon puta. From table and figure it is indicated that the annulus formation occur in the month of Apr. and this means that the annual rings were formed in the period of spring.
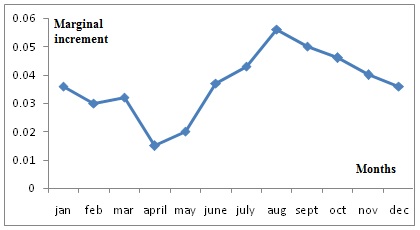 Figure 4: Monthly record of marginal growth for the scales of Terapon puta of Lake Timsah in Egypt.
Figure 4: Monthly record of marginal growth for the scales of Terapon puta of Lake Timsah in Egypt.| Month | Jan | Feb | Mar | Apr | May | June | July | Aug | Sept | Oct | Nov | Dec |
| No. of Fishes | 10 | 12 | 9 | 10 | 9 | 10 | 7 | 9 | 11 | 13 | 10 | 10 |
| MarginalIncrement(mm) | 0.036 | 0.030 | 0.032 | 0.015 | 0.020 | 0.037 | 0.043 | 0.056 | 0.050 | 0.046 | 0.040 | 0.036 |
The age composition and growth
The growth of the studied fish was described by the von Bertalanffy model Von Bertalanffy [7] based on the back-calculated length at age data (Figure 5). The estimated growth function was:
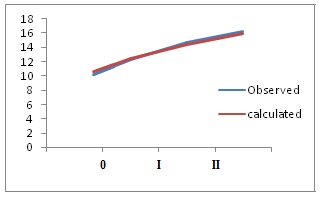 Figure 5: The von Bertalanffy growth curve of Terapon. puta in the lake Timsah, Egypt.
Figure 5: The von Bertalanffy growth curve of Terapon. puta in the lake Timsah, Egypt.Lt = 17.18 cm (1 - e-0.3632 (t +1.9363))
The growth constant (K) was estimated at 0.3632. However, the maximum theoretical length (L∞) and t0 describes the theoretical age where Lt is zero were 17.18 cm and -1.9363, respectively.
Growth in length
Body length-scale radius relationship:
L = 3.19644 +1.48960 S (r = 0.996)
Where L is the total length in cm and S is the scale radius in mm.
Back-calculations
LN = (L – 3.19644) Sn / S+3.19644
Where: LN is the length at the end of nth year, SN is the radius of the scale to nth annulus, S is the total radius of the scale and L is the total length at capture. From the data given in table 3, it is obvious that, Terapon puta attains its highest growth rate in the first year of life, after which a gradual decrease in growth increments was noticed with further increase in age.
| Age Group | MeanNumber | ObservedLength (cm) | Back Calculated Lengths | ||
| 1 | 2 | 3 | |||
| 0+ | 119 | 7.5 | 8.2 | ||
| I+ | 124 | 11.8 | 8.4 | 11.46 | |
| II+ | 93 | 14.3 | 7.4 | 11.18 | 13.8 |
| Average total | 335 | 8.0 | 11.63 | 13.8 | |
| Increment of length | 8.0 | 3.63 | 2.17 | ||
Length-weight relationship:
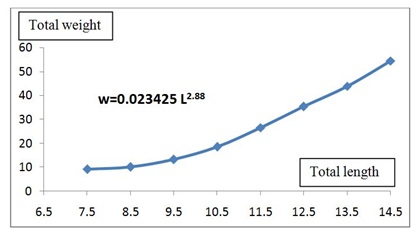 Figure 6: Length- weight relationship of Terapon puta off Lake Timsah in Egypt.
Figure 6: Length- weight relationship of Terapon puta off Lake Timsah in Egypt.Growth in weight
| Age Group | MeanNumber | Mean ObservationWeight (gm) | Back Calculated Weights | ||
| 1 | 2 | 3 | |||
| 0 | 119 | 10.13 | 8.71 | ||
| I | 124 | 31.69 | 11.27 | 28.47 | |
| II | 93 | 45.15 | 10.70 | 29.63 | 42.69 |
| Average total | 335 | 10.22 | 29.05 | 42.69 | |
| Increment of length | 10.22 | 14.17 | 17.96 | ||
The obtained results indicated that the growth rate in weight was slow during the first year of life. Then the annual growth increment in weight increased with further increase in age until it reached its maximum value at the end of the third year of life.
Mortality rates
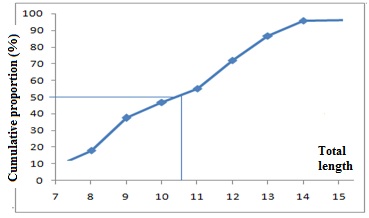 Figure 7: Cumulative curve from which length at first capture was determined.
Figure 7: Cumulative curve from which length at first capture was determined.Exploitation rate (E)
Length at first Capture (LC)
DISCUSSION
Age and back-calculated growth were determined from annual rings in the scales. Increase in length is rapid during the first year and slow thereafter. This study showed that the mean annual growth rate for 0+-II+ year's old fish ranged between 2.17 and 3.3 6 cm (Table 3).
The result of the growth rate in the first year of the small scaled Terapon puta reported in the present study is 8.0 cm. The same result may be obtained by Sabrah et al., [10]. The largest individual caught in the Lake Timsah were 14.6 cm Similar observation was made by Sabrah et al., [10] concluded that based on the number of rings on the otoliths, the oldest fish were 2 years old (14.2 cm) recorded in Lake Timsah. While Allen and Swainston [11] in Australia reported 16.0 cm as a maximum total length of Terapon puta.
The present study on the length-weight relationship of Terapon puta from the Lake Timsah coast has been studied. It is known that the relationship between length and weight has been studied in different fish species all over the world. The (b) values in fish is species specific and varies with sex, age, seasons, physiological conditions, growth increment and nutritional status of fish Bagenal and Tesch [12]. The relationship between total length and total body weight of Terapon puta was revealed highly correlation (r2 0.98) and the relationship was computed as w = 0.023425 L2.88. It is clear that the growth in weight of Terapon puta in lake Timsah was characterized by negative allometric growth (b < 3).The same result was obtained by Karna and Panda [13] who concluded that the value of exponent (b) of Terapon puta in Chilika Lagoon, Odisha (India) equal 2.76 as well Sabrah et al., [9] prove that the value of (b) of Terapon puta in Lake Timsah, Egypt equal 2.72. Also Nandikeswari and Sambasivam [14] finished to the exponent (b) equal to 2.0246 for males and 2.2074 for females. It is clear that, if b < 3, then large specimens have changed the body shape to become more elongated or small specimens were in better nutritional condition at the time of sampling Froese [15].
The von Bertalanffy growth parameters were estimated using scales of Terapon puta in Lake Timsah, Egypt (L∞: 17.18 cm, K: 0.3632 year-1 and t0: -1.9363 year). While the value of parameters reported by Sabrah et al., [10] was as L∞: 15.5 cm, K: 0.7 year-1 for Terapon puta in Lake Timsah, Egypt. The estimated parameters may vary as a function of a variety of factors such as region, year and methodology Goncalves et al. [16].
The exploitation rate of Terapon puta in the present study (E = 0.71) is higher than 0.50 of Gulland suggested that as a rule of thumb a fish stock is optimally exploited at a level of fishing mortality that generates E = 0.50 where optimum fishing mortality equal the natural mortality (F = M). Therefore, the stock of small scaled fish (Terapon puta) from the lake Timsah is being acutely over-exploited such observation noted also from the lake Timsah by Sabrah et al. [10]. The estimating total and fishing mortality rates in the lake Timsah with the exploitation rates were very high.
CONCLUSION
REFERENCES
- Nelson JS, Grande TC, Wilson MVH (2006) Fishes of the world. Wiley Online Library, New York, USA.
- Minos G, Imsiridou A, Economidis PS (2012) First record of Terapon theraps (Terapontidae) in the Aegean Sea (Greece). Cybium 36: 401-402.
- Sparre P, Ursin E, Venema SC (1989) Introduction to tropical fish stock assessment-Part 1: Manual. FAO Fisheries Technical Paper 306.
- Sparre P, Ursin E, Venema SC (1992) Introducion to tropical fish stock assessment-Part I: Manual. FAO Fisheries Technical Paper 306.
- Beverton RJ, Holt SJ (1957) On the dynamics of exploited fish populations. Limnology and Oceanography 19: 533.
- Ursin E (1967) A mathematical model of some aspects of fish growth, respiration and mortality. J Fish Res Bd Can 24: 2355-2453.
- Bertalanffy VL (1938) A quantitative theory of organic growth. Human Biology 10: 181-213.
- Gulland JA (1971) The fish resources of the Ocean. Fishing News, Cudham, Kent, UK. Pg no: 255.
- Allain V and Lorance P (2000) Age estimation and growth of some deep-sea fish from the north east Atlantic Ocean. Cybium 24: 7-16.
- Sabrah MM, Mohamedein LI, El-Sawy MA, Abou El-Naga EH (2016) Biological Characteristics in Approaching to Biochemical and Heavy Metals of Edible Fish Terapon puta, Cuvier, 1829 from Different Fishing Sites along the Suez Canal, Egypt. Journal of Fisheries and Aquatic Science 11: 147-162.
- Allen GR, Swainston R (1988) The marine fishes of North-Western Australia: A field guide for anglers and divers.Western Australian Museum. Perth, Western Australia.
- Bagenal TB, Tesch FW (1978) Age and growth. In: Bagenal TB (ed.). Methods for the assessment of fish production in freshwaters. Blackwell Scientific Publication. Oxford, England.
- Karna SK, Panda S (2012) Length-Weight Relationship (LWR) of 20 fish Species in Chilik Lagoon, Odisha (India). Asian J Exp Biol Sci Vol 3: 61-66.
- Froese R (2006) Cube law, condition factor and weight-length relationships: history, meta-analysis and recommendations. Journal of Applied Ichthyology 22: 241-253.
- Nandikeswari R, Sambasivam M (2016) Length-weight relationship of Terapon puta (Cuvier, 1829) from Puducherry waters. International Journal of Fisheries and Aquatic studies 4: 01-06.
- Goncalves JMS, Bentes L, Lino PG, Ribeiro J, Canario AVM, et al. (1997) Weight-length relationships for selected fish species of the small-scale demersal fisheries of the south and south-west coast of Portugal. Fisheries Research 30: 253-256.
Citation: El-Drawany M (2017) Age, Growth and Mortality of Terapon puta (Cuvier, 1829) in the Lake Timsah, Egypt. J Aquac Fisheries 1: 002.
Copyright: © 2017 Mohamed El-Drawany, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

