
Optimal Quarantine Duration for Preventing Epidemic with Window Period
*Corresponding Author(s):
Li QuSchool Of Economics And Management, Beijing Information Science And Technology University, Beijing, China
Tel:+86 10 6284 4802,
Email:quli@bistu.edu.cn
Abstract
The epidemic is one of the leading threats worldwide. An epidemic is the rapid spread of infectious disease and may be termed a pandemic which will lead to a disastrous consequence to human society. One way to prevent this from happening is quarantine. This study proposes a model to solve the optimal quarantine duration for epidemic with window period. The proposed model considered three different situations of quarantine to minimize the expected total cost of quarantine policy for an individual. This study provides a method to assist managing the people movement from the epidemic areas to other areas.
INTRODUCTION
The epidemic is one of the leading threats worldwide [1]. An epidemic is the rapid spread of infectious disease to a large number of people in a given population within a short period of time, usually two weeks or even less. For example, in meningococcal infections, an attack rate in excess of 15 cases per 100,000 people for two consecutive weeks is considered an epidemic [1,2].
An epidemic may be restricted to one location; however, if it spreads to other countries or continents and affects a substantial number of people, it may be termed a pandemic [1], which will lead to a disastrous consequence to human society. Though some epidemic can be easier to control as any infected person can be easily identified by its symptom, some other epidemic is more difficult due to the existence of a window period , during which there may be no obvious symptom and it is difficult to identify whether one if infected, such as tuberculosis [3] and hepatitis [4,5]. In case of this, a classical policy has been widely used: people from an epidemic area who arrive other areas should be quarantined for a period of time to make sure whether they are infected so that the epidemic can be controlled by cutting the networks off [6-9].
However, there is an issue about how to determine the quarantine duration. Generally, long quarantine duration can increase the probability of detecting infection but also cause some interruption to economic activities, whereas the short quarantine duration may fail to identify an infected person as infected and thus the person may be released such that it can infect more people. Herein, this study proposes a model to optimize the quarantine duration for epidemic with window period. This paper is arranged as follows. Section 2 proposes several assumptions. Section 3 presents the modeling process. Section 4 concludes this study.
ASSUMPTIONS
In this paper, we study the optimal quarantine duration for epidemic with window period. The problem considered here is described as following. Briefly, people from a certain area where epidemic outbreaks may be infected. Herein, a person from this area should be quarantined for a period of time to prevent others from the infection by this person. Based on the problem, the following assumptions are proposed for the model.
1) There is a window period with random duration w between the infection and the display of detectable symptom.
2) The window period of the infectious disease follows Weibull distribution with scale parameter λ and shape parameter Κ.
3) The cost that an infected person is detected is Cd , only including the treatment cost.
4) The cost that an infected person is undetected is Cu , including the treatment cost and the harm to society.
5) The cost that an uninfected person is quarantined per unit time is Cq , which is caused by the interruption to its economic activities.
THE MODEL
Since Weibull distribution is widely used in risk analysis [10-12], in this study it is used to model the probability distribution function of the window time from the infection to the display of detectable symptom for a person, which is
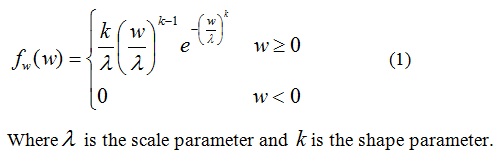
In addition, the pdf of the time from the infection to the start of quarantine is also a random variable v. Here, for illustration purpose, it is assumed that v is uniformly distributed between 0 and w. According to equation (1), the pdf of r, the time from quarantine beginning to the display of detectable symptom, can be further expressed, as
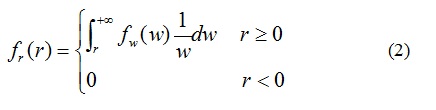
There are three situations for quarantining a person: 1). an infected person is detected; 2). an infected person is undetected; 3). an uninfected person is quarantined. Then, if the quarantine duration is q and the probability that a person from epidemic area is infected is pi , the probability and the expected cost of the three situations can be expressed as below.


CONCLUSION
This study proposes a model to solve the optimal quarantine duration for epidemic with window period. In the proposed model, three different situations of quarantine are considered. The expected total cost of quarantine policy for an individual is the objective to be minimized. This study provides a method to assist managing the people movement from the epidemic areas to other areas.
REFERENCES
- Centers for Disease Control and Prevention, Principles of Epidemiology, (2012) Third Edition. Atlanta, Georgia.
- Green MS, Swartz T, Mayshar E, Lev B, Leventhal A, et al . (2002) When is an epidemic an epidemic. Isr Med Assoc J 4: 3- 6.
- Gao K, Peng R, Wu D, Zhai Q (2019) Cox survival model based optimal screening strategy for tuberculosis. Prognostics and System Health Management Conference - 2019 Qingda.
- Fu B, Wang W, Shi X (2015) Impact of delayed diagnosis time in estimating progression rates in hepatitis C virus-related cirrhosis and death. Stat Methods Med Res 24: 693-710.
- Fu B, Wang W, Shi X (2012) A risk analysis based on a two-stage delayed diagnosis regression model with application to chronic disease progression. European Journal of Operational Research 218: 847- 855
- Keeling MJ, Eames KTD (2005) Networks and epidemic models. Journal of The Royal Society Interface 2: 295- 307.
- Newman MEJ (2002) Spread of epidemic disease on networks. Physical Review E 66: 016128
- Moreno Y, Pastor-Satorras R, Vespignani A (2002) Epidemic outbreaks in complex heterogeneous networks. The European Physical Journal B - Condensed Matter and Complex Systems 26: 521-529.
- Gao K, Peng R (2019) The Model of Venereal Disease Transmission Among Male Homosexuals Considering Multiple Channels. Current Findings of Infectious Disease: 1-6.
- Peng R, Hu QP, Ng SH, Xie M (2010) Testing effort dependent software FDP and FCP models with consideration of imperfect debugging. Fourth International Conference on Secure Software Integration and Reliability Improvement.
- Peng R, Li YF, Liu Y (2018) Reliability of multi-release open-source software, Software Fault Detection and Correction: Modeling and Applications 75-94.
- R Peng, YF Li, WJ Zhang, QP Hu (2014)Testing effort dependent software reliability model for imperfect debugging process considering both detection and correction, Reliability Engineering [?] System Safety126: 37- 43.
Citation: Gao K, Chen G, He Q, Qu Li, Ma Ye, et al. (2020) Optimal quarantine duration for preventing epidemic with window period. J Infect Non Infect Dis 5: 028.
Copyright: © 2020 Li Qu, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

